Розробка уроку на тему "РОЗВ’ЯЗУВАННЯ ЛОГАРИФМІЧНИХ РІВНЯНЬ"

Державний навчальний заклад

«Мукачівський центр професійно-технічної освіти»

Відкритий урок з математики

(II курс)

ТЕМА «РОЗВ’ЯЗУВАННЯ ЛОГАРИФМІЧНИХ РІВНЯНЬ»

Предмет. Математика

Тема програми.  Показникова та логарифмічна функції.

Тема уроку.  Розв’язування логарифмічних рівнянь.

Мета уроку:

навчальна - систематизувати методи розв’язування логарифмічних рівнянь, удосконалити вміння і навички розв’язування логарифмічних рівнянь, розглянути типові помилки, що допускають учні при розв’язуванні рівнянь, показати важливість даної теми, активізувати мислення учнів через різні форми та методи роботи;

розвиваюча - розвивати творче, креативне мислення учнів; сприяти розширенню навичок роботи із онлайн ресурсами та навичок самоконтролю;

виховна - виховувати інтерес до математики; створювати ситуацію успіху для формування позитивного ставлення до себе «я можу, у мене все вийде».

Тип уроку: повторення.

Вид уроку:  урок повторення з використанням інтерактивних технологій.

Форми проведення: словесні, наочні, практичні.

Методи організації навчальної діяльності: фронтальні, групові, індивідуальні.

Комплексно-методичне забезпечення: технічні засоби навчання: ПК, мультимедійний проектор, екран; дидактичні засоби: картки із завданнями для письмової роботи, таблиці; наочність: мультимедійна презентація для супроводу уроку.

Хід уроку

І. Організаційний момент.

Перевірка явки учнів та готовності  їх до уроку.  Оголошення теми та мети уроку.

II. Мотивація навчальної і пізнавальної діяльності

Не всі учні люблять математику. Деякі учні, а то і дорослі,  вважають, що це суха і нецікава наука. Доведемо протилежне. Покажемо взаємозв'язок математики з іншими предметами; покажемо, що математика – не тільки строга система  законів, правил та задач, але і унікальний засіб пізнання краси. Сьогодні ми з вами поринемо в світ чудовий та прекрасний – в світ математичних рівнянь.

Розпочнемо наш урок словами Джорджа Пойя:

«Уміння розв’язувати математичні задачі— практичне мистецтво, подібне плаванню, або катанню на лижах, або грі на фортепіано: навчитися цьому можна, лише постійно тренуючись...»

Аутотренінг

• Я – учень.
• Я – особистість творча.
• Я думаю, аналізую.
•  Я не боюсь помилитись.

 Помилившись,  міркую далі.

 Шукаю істину.

•  Я вірю в свої сили.
•  Я хочу знати.

III. Актуалізація опорних знань

Французький письменник Анатоль Франс (1844-1924) помітив, що: «Навчатися можна весело, з гарним настроєм, посміхаючись… Щоб переварити знання, потрібно поглинати їх з апетитом».

Прислухаємося до поради письменника: будемо на уроці активними, уважними і «поглинати» знання будемо з великим бажанням, адже вони скоро нам знадобляться для успішного виконання контрольної роботи, а в подальшому і успішної здачі ЗНО.

1. Рефлексія настрою та емоційного стану «Смайлик»

Викладач. Оберіть смайлик, який відповідає вашому настрою. Надіюсь ваш настрій чудовий, сповнений бадьорості та активності. Адже лише гарний настрій підвищує працездатність, впливає на самопочуття, надає впевненості в собі, допомагає впоратися з складними ситуаціями.

2. Рекламна пауза

Відомий учений Альберт Енштейн  так висловлювався про логарифми:

«Мені доводиться ділити свій час між політикою та рівняннями. Проте рівняння, як на мене, набагато важливіше, тому що політика існує тільки для даного моменту, а рівняння будуть існувати вічно».

3. Телегра «Випадкове колесо «Логарифми»»

https://wordwall.net/ru/resource/25009301

IV. Удосконалення вмінь і навичок

При розв’язуванні логарифмічних рівнянь досить часто доводиться виконувати не рівносильні перетворення, які можуть призвести до появи сторонніх коренів. Тому обов’язково виконуємо перевірку.

«Рівняння – це золотий ключ, що відкриває усі математичні сезами».

(польський математик С. Коваль)

Скажи мені – і я забуду,

Покажи мені – і я запам'ятаю,

Дай мені діяти самому – і я навчуся.

Давньокитайська мудрість

1. Виконання письмових вправ

Групове виконання завдань під керівництвом викладача «Аукціон логарифмічних рівнянь». Здобувачі освіти поділяються на 3 групи для розв’язку логарифмічних рівнянь:

Червоний колір – високий рівень

Зелений колір – достатній рівень

Синій колір – початковий та середній рівні

Час на виконання 10 хв.

Синій колір

Розв’язок:

1. ОДЗ: х>0;

x=3^-2

x=

Відповідь: x=

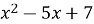2. ОДЗ: >0

D=(-5)²-4·7=25-28<0

Коренів не має, графіком даної функції є парабола з вітками направлених вгору, яка набуває додатного значення при будь-яких х.

=3

=0

За теоремою Вієта:

х₁+х₂=5

х₁·х₂=4

х₁=1

х₂=4

Відповідь: х₁=1, х₂=4

3. ОДЗ: ⇒⇒⇒ ⇒

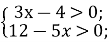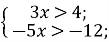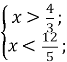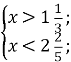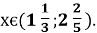
3х-4=12-5х

3х+5х=12+4

8х=16

х=2

Відповідь: x=2.

Зелений колір

Розв’язок:

1.                   ОДЗ: 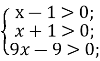⇒ ⇒ 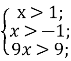⇒ 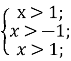xє(1+;∞)

lg((x-1)·(x+1))=lg(9x-9);

(x-1)·(x+1)=9x-9;

x²-1=9x-9;

x²-9x+9-1=0;

x²-9x+8=0;

За теоремою Вієта:

х₁+х₂=9;

х₁·х₂=8;

х₁=1 ∉ ОДЗ;

х₂=8

Відповідь: х=8.

2. ОДЗ: х>0;

Нехай log₄x=t, тоді

t²-3t+2=0;

За теоремою Вієта:

t₁+t₂=3;

t₁·t₂=2;

t₁=1;

t₂=2.

log₄x=1      log₄x=2

x=4       x=4²

        x=16

Відповідь: х₁=4, х₂=16.

Червоний колір

Розв’язок:

1. ОДЗ: х>0;

Нехай log₃x=t, тоді

t²+t-2=0;

За теоремою Вієта:

t₁+t₂=-1;

t₁·t₂=-2;

t₁=-2∉ ОДЗ;

t₂=1.

log₃x=1

x=3

Відповідь: х=3.

2.     ОДЗ: х>0;

;

x=16.

Відповідь: х=16.

4. «Хвилинка ерудита» (опитування з використанням навчальної платформи Кahoot.it)

https://create.kahoot.it/details/7940da8a-ab2d-4d9e-af8b-8b103ad5ae15

Пригадаємо властивості логарифмів.

• Чому дорівнює логарифм одиниці? (0).
• Чому дорівнює логарифм основи? (1).
• Назвіть основну логарифмічну тотожність. ()
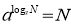• Чому дорівнює логарифм добутку двох додатних чисел? (…дорівнює сумі логарифмів)
• Чому дорівнює логарифм частки двох додатних чисел? (…різниці логарифмів діленого і дільника)
• Чому дорівнює логарифм степеня додатного числа? (…показнику степеня, помноженому на логарифм основи цього степеня)
• Чому дорівнює логарифм кореня з додатного числа? (…логарифму підкореневого виразу, поділеному на показник кореня)
• Якими є додатні числа, якщо логарифми таких чисел за тією самою основою рівня? (…рівні)

• Чи існує логарифм від’ємного числа? (Ні)
• Логарифм ще якого числа не існує? (0)
• Якою може бути основа логарифма? (тільки додатною, і  ≠1)

VI. Підведення підсумків уроку.

Отже, на уроці ви добре попрацювали, продемонстрували свої знання, вміння та навички, були активними.

VII. Домашнє завдання

«Поштові листи» Зараз прошу отримати поштові листи з домашнім завданням на свою електронну пошту.

Список використаної літератури:

1. Математика: алгебра і початки аналізу та геометрія рівень стандарту: підруч. для 11 кл. закладів загальної середньої освіти /А.Г. Мерзляк,

Д. А. Номіровський, В. Б. Полонський та ін. - Х.: Гімназія, 2019.-208с.

2. Алгебра і початки аналізу: проф. рівень: підруч. для 11 кл. закладів загальної середньої освіти / А.Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський та ін.-Х.: Гімназія, 2019.-352с.
3. Мерзляк А.Г. Алгебра. 11 клас : підруч. для загальноосвіт. навч. закл.: академ. рівень, проф. рівень / А.Г. Мерзляк, Д.А. Номіровський, В.Б. Полонський, М.С. Якір. – Х. : Гімназія, 2011. – 431 с. 
4. Алгебра і початки аналізу: навч. посібник для учнів проф.-техн. Навчальних закладів. М.І. Шкіль, З. І. Слєпкань, О.С. Дубинчук, К.: Техніка, 2000. –544 с. 
5. Алгебра i початки аналізу: Підруч. для 11 кл. загальноосвіт. навч. закладів / М.І. Шкіль, З. І. Слєпкань, О. С. Дубинчук К.: –Зодіак-Еко, 2006. –384 с. : іл.
6. Логарифмічні рівняння // Математика. – 2004. – квітень (№ 14). с.7-10.