Розробка уроку на тему "Відсотки."

Тема. Відсотки.

Мета: сформувати в учнів поняття про відсоток; вміння записувати відсотки десятковими і звичайними дробами.

Тип уроку: засвоєння нових знань

Хід уроку

І. Розминка

Усні вправи

1. Знайдіть 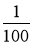від числа: 1) 200; 2) 60; 3) 7; 4) 67,3; 5) 5,48.
2. У саду росло 300 дерев, 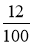від них становлять яблуні. Скільки яблунь росло в саду?
3. У школі навчається 900 учнів, з них 0,15 отримали за рік з математики 11 балів. Скільки учнів отримали 11 балів з математики?
4. Виконайте множення на 0,01: 1)3; 2) 11; 3)100; 4) 1000; 5) 123.

II. Актуалізація опорних знань

Запитання до класу

Яку частину становить?

1) 1 ар від 1 гектара;   2) 1 м² від 1 ара; 3) 1 см від 1 м;

4) 1 копійка від 1 гривні;  5) 1 рік від 1 століття.

[Відповідь — ]

III. Формування знань

Бесіда

Друзі! Сподіваюсь, ви помітили, що в повсякденному житті часто маємо справу із сотими частинами величин: 1 ар = га, 1м² = а, 1 см = м,   1 к = грн. Тому для цього часто вживаного дробу 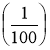дібрали спеціальну назву й позначення: 1 відсоток («від ста»), позна­чається 1 % і = 0,01 = 1 %.

Тобто відсотки — це особлива форма запису дробів.

Тому можна перетворювати відсотки у дроби: 1 % = 0,01,

2% = 2 · 0,01 = 0,02;

15% = 15 · 0,001 = 0,15;

100% = 100 · 0,01 = 1;

125% = 125 · 0,01 = 1,25.

Маємо: щоб записати відсотки десятковим дробом, треба кількість відсотків помножити на 0,01 (поділити на 100), при цьому 100 % = 1!

Також можна розв'язувати обернену задачу: будь-який десятковий дріб записати у вигляді відсотків: знаючи, що 1 = 100%, можемо сказати, що

2 = 2 · 1 = 2 · 100 % = 200 %;  0,3 = 0,3 · 1 = 0,3 · 100%; = 30 %;

0,125 = 0,125 · 1 = 0,125 · 100 % = 1,25.

Висновок: будь-яке число можна виразити у відсотках і навпаки; будь-яку кількість відсотків можна виразити десятковим дробом.

Але зазвичай записом у формі відсотків користуються, коли мають справу із сотими частими величинами.

Згадаймо, що:

1 а дорівнює 1 % від 1 га; 1 м² дорівнює 1 % від 1 а і т. д.

Закріплення

Що складає?

1) 1% гривні; 2) 1% центнера; 3) 1% дециметра; 4) 1% кілометра. Тобто, щоб знайти 1% будь-якої величини, треба поділити значення цієї величини на 100.

IV. Формування вмінь

Розв'язування вправ

1. Запис відсотків десятковим або звичайним дробом: №№ 1026; 1030.
2. Запис десяткового дробу у відсотках: № 1028.
3. Наочні уявлення про відсотки: № 1024 (а-в), 1025.

При розв'язуванні № 1025 (8) слід звернути увагу, що 100% площини квадрата — це і є весь квадрат!!!

4. Задачі на повторення: № 1048.

V. Підсумок уроку
Запитання до класу

1. Що більше: 1 % від гривні чи 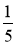від 5 копійок?
2. Який з наступних записів є записом 3% у вигляді десяткового дробу?

1) 3; 2) 0,3; 3) 0,03; 4) 0,003.

VI. Домашнє завдання

п. 34, №№ 1027; 1029; 1024 (г, д, є), на повторення 1044 (1).