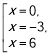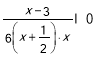Розробка уроку "Розв’язування нерівностей методом інтервалів"

 

Тема уроку: Розв’язування нерівностей методом інтервалів

 

Мета уроку : 

• організувати роботу по сприйняттю, осмисленню і первинному закріпленню навичок у розв’язуванні нерівностей методом інтервалів, розвивати у учнів навички творчого підходу до рішення завдань;
• сприяти формуванню уміння розв’язувати квадратичні нерівності  і оформлення нерівностей методом інтервалів, домогтися раціонального використання набутих знань; 
• виховувати пізнавальну активність, сприяти розвитку логічного мислення, математичної і загальної грамотності.

 

Обладнання і матеріали : комп'ютер, проектор, екран, презентація для супроводу зайняття, індивідуальні картки для учнів.

Очікувані результати: учні повинні вміти розв’язувати нерівності методом інтервалів і розуміти, коли можна застосовувати цей метод.

Тип уроку: урок засвоєння нових знань.

Методи: словесні: розповідь, бесіда,  коментар до виконання вправ, використання ключових слів, методи мотивації, збудження інтересу;

Практичні: розв’язування вправ,  метод повторення, виконання вправа за зразком, поступового ускладнення завдань.

Хід уроку

 

I. Організаційний етап

▪ Привітання

Доброго дня, шановні учні! Ще 2400 років тому китайський педагог Конфуцій сказав: «Те, що я чую - я забуваю. Те, що я бачу і чую – я трохи пам’ятаю. Те, що я чую, бачу і обговорюю – я починаю розуміти. Коли я чую, бачу, обговорюю і роблю – набуваю знань і навичок».

 Тож, запрошую вас до співпраці.

▪ Перевірка готовності учнів та  до уроку.

 

II. Перевірка домашнього завдання

▪ Перевірка письмового завдання біля дошки

 

III. Формулювання мети й завдань уроку, мотивація навчальної діяльності

▪ Оголошення теми уроку

▪ Формулювання разом з учнями мети й завдань уроку

▪ Мотивація навчальної діяльності

     Ви вже знаєте два види нерівності : лінійне і квадратне. Для кожного з них існує свій спосіб розв’язання. У старших класах ви познайомитеся ще з декількома видами нерівностей, такими як тригонометричні нерівності, показові, логарифмічні, раціональні, ірраціональні. Кожна з цих нерівностей теж матиме свій спосіб рішення. Але сьогодні на уроці я познайомлю вас з універсальним способом розв’язання нерівностей, який називається метод інтервалів. З його допомогою ви зможете розв’язати будь-яку нерівність. Навіть якщо ви забудете спосіб, яким вирішується то або інша нерівність, то завжди зможете скористатися методом інтервалів.

    Відкриваємо робочі зошити. Записуємо число, тему уроку : "Розв’язування нерівностей методом інтервалів". Розв’язування нерівності ми робитимемо по алгоритму, який записаний на дошці.

 

IV. Актуалізація опорних знань

▪ Усні вправи

1. Розв’яжіть нерівність:

а) 9х² > 0;    б) 4х² ≥ 0;    в) х² -10х +25 ≤ 0;    г) (х - 1)(х - 2)<0.

 

2. Знайдіть область визначення функції:

а) ;       б)

 

     3 . Розкладіть на множники квадратний тричлен:

          а) х² – х -12 ; б) х² -3х -4;       в) х² +9х +18 . 

 

 V. Засвоєння нових знань.

 

1. Схема розв’язування нерівності методом інтервалів :

 1. Привести нерівність до такого виду, де в лівій частині знаходиться функція, а в правій 0.

 2. Знайти область визначення функції.

 3. Знайти нулі функції, тобто - вирішити рівняння, х₁ = m, x₂ = n.

 4. На числову пряму нанесемо область визначення функції і за допомогою нулів розіб’ємо її (область визначення) на інтервали.

 5. Визначити знаки функції на отриманих інтервалах.

 6. Вибрати інтервали, де функція набуває необхідних значень і записати відповідь.

Виходячи з вищезазначеного, маємо розв’язки нерівностей:

2. Застосування методу інтервалів на прикладах.

 

Методичний прийом „Працюємо за зразком”.  Разом з учнями розв’язуємо нерівність методом інтервалів з коментуванням.

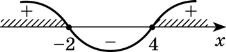
а) Розв’яжемо нерівність  (х + 2)(х - 3)(х - 5) >0.

Розглянемо функцію  у = (х + 2)(х - 3)(х - 5)  і знайдемо ті значення x, при яких вона набуває додатних значень. Область визначення функції — множина дійсних чисел. Нулі функції: х₁=-2, х₂=3, х₃=5. Нулі розбивають область визначення на чотири проміжки: (); (-2; 3); (3; 5); (5; +  . На будь-якому з цих проміжків кожен із множників х + 2, х - 3, х - 5   має певний знак. Позначимо на координатній прямій нулі функції та її знаки на кожному з проміжків.

Відповідь: (-2; 3) .

На кожному з проміжків функція зберігає знак, а після переходу через нулі її знак змінюється. У такий спосіб можна знайти знаки функції виду

f(x) = (х – х₁)(х – х₂)(х – х₃)…(х - х_n)

 

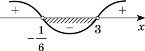
б) Розв’яжемо нерівність  3х² – 6х + 24 < 0.

 Зведемо нерівність до нерівності виду: 3(х + 2)(х - 4)

х₁ = -2,         нулі функції

х₂ = 4

Позначимо на координатній прямій нулі фу

функції, розіб’ємо її на інтервали, Відповідь: (-2; 4).

 

в) Розв’язування дробових раціональних нерівностей.

Метод інтервалів можна застосовувати і для розв’язування дробових нерівностей. Дробово-раціональна функція може міняти знак тільки в тих точках, в яких вона дорівнює нулю або не існує.

Приклад 1.

 

Розв’язання:

Розглянемо функцію:

 

 

D(f): х

Нулі функції: х₁ =-15, х₂ = 2

Наносимо на координатний промінь нулі функції і ОДЗ, визначимо знак функції на отриманих інтервалах, виберемо інтервал, де функція набуває додатних значень.

Відповідь:

 

Приклад 2. Що робити, якщо чисельник або знаменник не вдається розкласти на лінійні множники? Розглянемо таку нерівність:

 <0

Квадратний тричлен х² - 4х +7 на множники розкласти не можна: D< 0, коренів не існує. Це означає, що знак виразу  х² - 4х +7 при всіх дійсних х

має однаковий знак, тобто додатній.

Поділимо обидві частини нерівності на вираз х² - 4х +7 і приведемо к рівносильній нерівності:

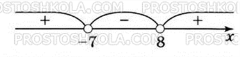
< 0, яку легко розв’язати методом інтервалів

 

Відповідь: (-7; 8)  

Зверніть увагу - ми поділили обидві частини нерівності на величину, про яку точно знали, що вона позитивна. Звичайно, в загальному випадку не варто множити або ділити нерівність на змінну величину, знак якої невідомий.

 

VI. Закріплення знань

▪ Робота з підручником біля дошки: № 216

▪ Індивідуальна робота за картками

Учні, які добре засвоїли пояснення матеріалу, виконують роботу за картками:

 

Картка 1 Використовуючи метод інтервалів, розв’яжіть нерівність: а) ;   в) ; б) ;   г) . Алгебра, 9 клас. Урок №28

 

Картка 2 Використовуючи метод інтервалів, розв’яжіть нерівність: а) ;    в) ; б) ;   г) . Алгебра, 9 клас. Урок №28

 

Розв’язок до карток

Картка 1
а) ; ; ; — нулі функції. Відповідь: .	б) ; ; ; ; — нулі функції. Відповідь: .	в) ; ; : ; — нуль функції. Відповідь: .	г) ; ; ; ; ; ; ; : ; — нуль функції. Відповідь: .

 

Картка 2
а) ; ; ; ; — нулі функції. Відповідь: .	б) ; ; ; — нулі функції. Відповідь: .	в) ; ; ; : — нуль функції. Відповідь: .	г) ; ; ; : ; — нулі функції. Відповідь:

 

VII. Підбиття підсумків уроку

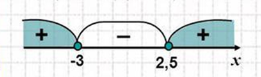Знайди помилку:

а) (2х -5)(х + 3)≤ 0;

Відповідь: (-)

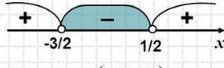
б)  4х² +4х -3 > 0   

 

Відповідь:

 

До сьогоднішнього уроку ви уміли вирішувати квадратичні нерівності тільки одним способом, сьогодні ви познайомилися з методом інтервалів. Який з цих способів вам прийнятніше для вирішення квадратичних нерівностей? Надалі кожен з вас вирішуватиме нерівності тим способом, який йому більше подобається.

 

VIII. Домашнє завдання, інструктаж щодо його виконання

▪ Завдання для всього класу

Підручник __________________________________________________ 

▪ Індивідуальне завдання

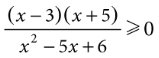Розв’яжіть нерівність .