Середнє арифметичне. Середні величини.

Тема. Середнє арифметичне. Середні величини.

Мета: сформувати вміння знаходити середнє арифметичне і розв'я­зувати вправи на застосування цього поняття.

Тип уроку: засвоєння навичок і вмінь.

Хід уроку

І. Актуалізація опорних знань. Розминка

Усні вправи

1. Подвойте суму 2,4 + 19,7 + 7,3 + 4,6.
2. Знайдіть чверть різниці 6,2 – 3,4.
3. Знайдіть число, якщо його п'ята частина дорівнює добутку 1,8 · 5.
4. Порівняйте числа:

1) і 0,51; 2) і 0,8; 3) 0,4 і ; 4) і 0,4; 5) і 0,49999;

6) і ; 7) і ; 8) і ; 9) і .

5. Розв'яжіть рівняння:
   1)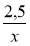 = 0,5; 2) 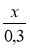= 0,4; 3) 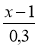= 0,4.

II. Формування знань

Постановка проблеми

Задача 1. Протягом червня тітка Горпина на своєму городі зібрала 124 кг полуниць.

Скільки кілограмів полуниць збирала вона щодня, якщо:

1. щодня врожай був однаковим;
2. невідомо чи був врожай однаковим щодня?

Розв'язання

1) Зрозуміло, що якщо кожного з 31 днів червня врожай був однаковим, то кожного дня він становить 124 : 31 = 4 (кг).

2) У цьому випадку неможливо точно відповісти на запитання, бо мож­ливі різні випадки. Але середнє значення врожаю 124 : 31 = 4 (кг).

Задача 2. Загальний вік гравців футбольної команди 286 років. Якого віку кожний з гравців, якщо:

1) вони однолітки;

2) невідомо, чи всі вони однолітки?

Розв'язання

1) 286 : 11 = 26 (років) — вік кожного гравця;

2) відповісти на запитання точно неможливо, тому говорять, що се­редній вік гравців футбольної команди 286 : 11 = 26 років.

Розв'язання проблеми

Після розбору задач 1 і 2 вчитель робить висновки.

Отже, досить часто у повсякденному житті ми маємо справи з се­редніми величинами (середня врожайність, середня зарплата вчителя, се­редня кількість окладів за місяць, рік і т. д.). Але як знайти середнє зна­чення величини, ми розглянемо наступного уроку. А от з окремим випадком середніх величин — середнім арифметичним, ми познайоми­мося сьогодні.

Задача 3. Туристи за 1-шу годину пройшли 2,6 км. За другу — 3,3 км, а за третю — 2,5 км. З якою сталою швидкістю (середньою швидкістю) треба було їм йти, щоб пройти всього відстань за 3 год?

Розв'язання.

Очевидно, що = 8,4 : 3 = 2,8 (км/год).

Отже, бачимо, що для знаходження відповіді задачі ми знайшли суму 3-х доданків і поділили її на 3 (кількість доданків). Отже, середнім арифметичним кількох чисел називають частку від ділення суми цих чисел на кількість доданків.

Приклад 1. Знайдіть середнє арифметичне чисел 23,4; 18,7; 19,6 і 20,8.

Розв'язання.

Середнє арифметичне дорівнює:

.

Приклад 2. Середнє арифметичне чисел 3,7 і х дорівнює 2,15. Знайдіть число х.

Розв'язання

; 3,7 + х = 21,5 · 2; 3,7 + х = 4,3; х = 4,3 – 3,7; х = 0,6.

III. Формування вмінь

Учні розв'язують за аналогією з прикладами 1 і 2 №№ 997; 998; 1003, а також виконують вправи на повторення: №№ 1015(1); 1016.

IV. Підсумок уроку

Розв'язуючи усні завдання, учні повторюють основні теоретичні відо­мості уроку (означення середнього арифметичного кількох чисел) і пе­ревіряють свої уміння знаходити середнє арифметичне.

Яке з чисел більше?

1. 12 чи середнє арифметичне 11 і 14;
2. середнє арифметичне 7 і 8 чи середнє арифметичне 10, 9 і 6;
3. середнє арифметичне 19, 11, 13 і 15 чи середнє арифметичне 12, 14, 16 і 18.

V. Домашнє завдання

п. 33, №№ 1000; 1004; 1015 (2); 1018 (1).