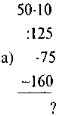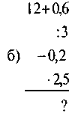Скорочення звичайних дробів
Тема. Скорочення звичайних дробів
Мета: сформувати уявлення учнів про зміст поняття скорочення дробів та навчити користуватися цими уявленнями для виконання завдань, що передбачають скорочення дробів та дробових виразів (вигляду ![]() )
)
Тип уроку: засвоєння знань; застосування вмінь і навичок.
Хід уроку
І. Перевірка домашнього завдання. Актуалізація опорних знань
Особливу увагу слід звернути на вправи такого типу (див. нижче), бо ці вправи є базовими і завдання подібного типу передбачені в самостійній роботі.
- Замініть х таким числом, щоб була правильною рівність:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Виразіть у хвилинах:
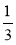 від 2 год 30 хв;
від 2 год 30 хв; 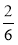 від 2 год 30 хв. Результати порівняйте.
від 2 год 30 хв. Результати порівняйте.
Усні вправи (фронтальна робота)
- Обчисліть:
|
|
|
- Знайдіть НСД і НСК чисел: а) 3 і 4; б) 3 і 6; в) 6 і 9.
-
Дано дріб:
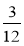 .
.
а) Помножте чисельник і знаменник цього дробу на 2; на 10. Які результати ви дістали?
б) Поділіть чисельник і знаменник дробу на 3. Який результат ви дістали?
в) Чи можна даний дріб записати у вигляді іншого дробу зі знаменником 24; 30? Чому?
г) Знайдіть х із рівностей: ![]() ;
; ![]() .
.
Для «сильних» і «слабких» учнів індивідуальна робота за картками
|
Картка № 1 (для «сильних») Як можна розрізати циферблат годинника на 6 частин так, щоб у всіх частинах сума чисел була однаковою? |
|
Картка № 2 (для «сильних») Запишіть, використовуючи три п'ятірки і знаки дій: 1) 1; 2)0; 3) 2; 4) 5. |
|
Картка № 3 (для «сильних») Як треба розставити знаки «+» у запису 1 2 3 4 5 6 7, щоб дістати в сумі 100? |
Картки-підказки (для «слабких»)
|
Користуючись прикладами закінчіть записи: |
|
|
|
|
II. Формування уявлень
Ви вже знаєте, що якщо чисельник і знаменник помножити або поділити на одне й те саме число, відмінне від 0, то значення дробу не зміниться. А зміниться запис цього дробу: стане більш «коротким» чи більш «довгим». Помножити чисельник і знаменник дробу на число можна в будь-якому разі. Але чи завжди можна знайти число, відмінне від 1, на яке можна було б поділити чисельник і знаменник дробу?
Більшість учнів після подібної бесіди можуть самі зробити правильні висновки. Завдання вчителя — вислухавши відповіді учнів, грамотно сформулювати відповідні властивості (див. конспект 8).
|
Конспект 8 |
|
|
Скорочення дробів |
|
|
1) Нехай с = НСД(а; b) і с ≠ 1, тоді: (a i b – взаємно прості). 2) Якщо: с = НСД(а; b) = 1,
то |
Приклад
1) Скоротіть дріб
НСД (33; 44) = 11, отже,
2) Дріб бо НСД (4; 5) = 1 |
Під час усної лічби скорочення можна виконувати поступово, але в будь-якому разі відповідь повинна бути нескоротним дробом.
І рівень
Усні вправи
Мета вправ — не тільки первинне закріплення матеріалу, а й найголовніше,— розвиток мовлення учнів. Тому треба вимагати від учнів пояснень, читати завдання і т. ін.
-
Поясніть рівності:
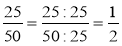 ;
; 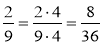 .
.
-
Скоротіть дроби:
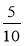 ;
; 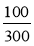 ;
; 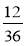 ;
; 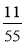 .
.
II, IIІ рівні
Письмові вправи
На цьому уроці слід звернути увагу на завдання зі скорочення дробів, щоб виробити в учнів спільне вміння скорочувати дроби. Тому й завдання підбираємо на скорочення з поступовим збільшенням складності завдань.
-
Скоротіть дроби:
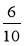 ;
; 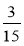 ;
; 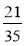 ;
; 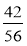 ;
; 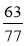 .
.
-
Знайдіть НСД чисельника і знаменника кожного із дробів та скоротіть дроби:
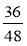 ;
; 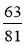 ;
; 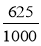 .
.
-
Запишіть звичайним нескоротним дробом:
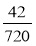 ;
; 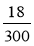 .
.
-
Скоротіть дроби: а)
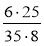 ; б)
; б) 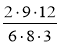 ; в)
; в) 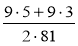 .
.
Методика розв'язування вправ
Ми з'ясували, що дріб можна скорочувати поступово, поділивши чисельник і знаменник спочатку на один, а потім на інший спільний дільник. Тому в таких дробах (див. завд. № 4) можна спочатку знайти один дільник (взяти якісь два числа в чисельнику і знаменнику, що мають СД ≠ 1), потім інший і поділити вирази в чисельнику і знаменнику Дробу поступово на один, а потім на інший дільник. Записи в зошитах можуть бути такими:
![]() — нескоротний дріб.
— нескоротний дріб.
У завданні 4 в) звернути увагу на те, що спочатку треба розкласти чисельник на множники (винести 9 за дужки), а потім, подібно до завдання 4 а) і б), розв'язати:
IV. Підсумки уроку
Що означає термін «скоротіть дріб»? Який дріб називається нескоротним?
Чи правильно виконано скорочення дробу ![]() ?
?
а) ![]() ; б)
; б) ![]() .
.
НСД(12; 16) = 4.
Який зі способів скорочення коротший?
Чи правильно виконано скорочення дробів?
![]() ;
; ![]() ;
; ![]() .
.
V. Домашнє завдання
-
Поясніть рівності:
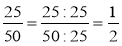 ;
; 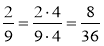 .
.
-
Скоротіть дроби:
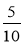 ;
; 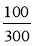 ;
; 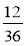 ;
; 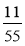 .
.
-
Знайдіть НСД чисельника і знаменника кожного із дробів та скоротіть дроби:
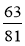 ;
; 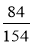 .
.
-
Запишіть звичайними нескоротними дробом:
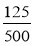 ;
; 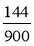 .
.
-
Виразіть у кілограмах і запишіть звичайним нескоротним дробом:
25 г; 125 г; 250 г; 160 г; 825 г; 950 г. -
Знайдіть, НСК знаменників дробів: а)
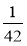 і
і 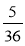 ; б)
; б) 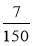 і
і 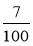 ; в)
; в) 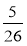 і
і 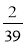 .
.


про публікацію авторської розробки
Додати розробку