Стаття "Методи швидких обчислень"
МЕТОДИ ШВИДКИХ ОБЧИСЛЕНЬ
Актуальність теми. Найважливішим завданням навчання математики є забезпечення міцного і свідомого оволодіння математичними знаннями та вміннями, потрібними в повсякденному житті і в роботі кожного члена сучасного суспільства. Обчислювальна культура є тим запасом знань і умінь, який знаходить постійне застосування, є фундаментом вивчення математики та інших навчальних дисциплін. Крім того, обчислення активізують пам’ять, увагу, прагнення до раціональної організації діяльності.
Звичка виконувати усно нескладні обчислення і викладення нерідко породжує потребу виробляти уявні експерименти при вирішенні завдань, висловлювати здогади, припущення про шляхи вирішення більш складних завдань, подумки (усно) перевіряючи істинність припущень.
Виникає потреба в ознайомленні з додатковими прийомами усних та письмових обчислень, які дозволили б значно скоротити час, витрачений на обчислення і запис розв’язку, і уникнути використання різних обчислювальних засобів.
Мета роботи:дослідити деякі способи використання прийомів швидкого рахунку.
Для реалізації цієї мети необхідно вирішити такі завдання:
1) вивчити способи швидких обчислень в різних етапах розвитку математики;
2) розглянути різні прийоми швидкого рахунку як способу вирішення досліджуваної проблеми;
3) перевірити ефективність запропонованих методів.
Об’єктом дослідження є процес навчання математики в основній школі.
Предмет дослідження — формування та розвиток обчислювальної культури засобами системи вправ для швидкого рахунку.
РОЗДІЛ 1 МЕТОДИ ШВИДКИХ ОБЧИСЛЕНЬ З ІСТОРІЇ МАТЕМАТИКИ
1.1 Українська народна математика.
Ми багато вчили з народознавства про культуру нашого народу, про його звичаї, одяг. Але як українці в своєму побуті використовували математику, залишається для нас ще не зовсім дослідженою загадкою.
Серед українців побутувало поважне ставлення до освіти, батьки намагалися будь-що віддати своїх дітей у науку. Впродовж віків у народному середовищі виробилися оригінальні способи виконання арифметичних дій, розвитку логічного мислення. Математичні відомості українського народу мало досліджені не лише істориками математики, але і етнографами. Однак ця галузь знань дає цінний матеріал для вивчення розвитку культури українського народу. Значного розвитку математичні знання набули ще в часи Київської Русі. Незважаючи на всю різноманітність лічби, основною системою числення в українців була десяткова.
Археологічні пам’ятки свідчать, що вже у IX—X ст. східні слов’яни застосовували прості прийоми лічби. У ХVШ-ХІХ ст. способи лічби поступово удосконалювалися, хоч подекуди серед населення залишились у вжитку обчислення, що виникли у давнину. Деякі селяни дуже швидко і правильно обчислювали на пальцях, особливо дію множення.
Наприклад, 7 ![]() 9. На одній руці загинаємо стільки пальців, наскільки 7 більше 5, тобто загинаємо 2 пальці. На другій — на скільки 9 більше 5, тобто загинаємо 4 пальці. Отже, на одній руці загнуто 2, не загнуто 3 пальці; на другій руці загнуто 4 пальці, не загнутий 1 палець. Далі знаходимо число усіх загнутих пальців 2 + 4 = 6 (це будуть десятки ) і знаходимо добуток числа не загнутих пальців 3
9. На одній руці загинаємо стільки пальців, наскільки 7 більше 5, тобто загинаємо 2 пальці. На другій — на скільки 9 більше 5, тобто загинаємо 4 пальці. Отже, на одній руці загнуто 2, не загнуто 3 пальці; на другій руці загнуто 4 пальці, не загнутий 1 палець. Далі знаходимо число усіх загнутих пальців 2 + 4 = 6 (це будуть десятки ) і знаходимо добуток числа не загнутих пальців 3 ![]() 1 = 3 (це будуть одиниці). У результаті одержуємо число 63. Цей спосіб описано у підручнику «Арифметика» Магницького, який вийшов у світ у 1703 р.
1 = 3 (це будуть одиниці). У результаті одержуємо число 63. Цей спосіб описано у підручнику «Арифметика» Магницького, який вийшов у світ у 1703 р.
Народна математика — сукупність народних математичних знань та навичок, в основі якої лежать потреби практичної діяльності (необхідність виконання різних арифметичних дій при проведенні землемірних робіт, зведенні житла та інших споруд тощо). Недоступність професійних математичних знань для широких верств українського населення у минулому зумовлювала удосконалення найпростіших традиційних прийомів лічби, вимірювання, способів зображення чисел.
На Україні найдавнішими засобами лічби були пальці рук, різні дрібні предмети. Так, при лічбі на пальцях, або, як називали, на колодочках, на одній руці було прийнято налічувати 15 «колодочок» з долоні та 15 — з іншої частини цієї ж руки. З предметів використовували картоплини, квасолинки, палички та ін. Для економії лічби існували числові групи: пара, трійка, п’ятка, десяток, копа тощо. Парами лічили худобу, птицю, хатнє добро (чоботи, підошви), трійками — нитки у прядиві (три нитки складали чисницю), п’ятками — снопи, десятками — яйця, гарбузи, кавуни, копами — яйця та снопи.
Арифметичні дії виконувалися усно. Існували своєрідні народні назви дій — додати, докласти, відкинуть, відлічить. Поширеним був спосіб додавання, коли спочатку додавалися сотні, потім десятки, а в кінці — одиниці. Множили шляхом повторного послідовного додавання. Ділення виконували, підбираючи частку послідовним повторним відніманням.
Приклади усного рахунку в давнину: на млин привезли спочатку 48 пудів, потім 95, а пізніше ще 117 пудів зерна. Щоб дізнатися, скільки всього зерна привезли на млин, мірошник підрахував: перший раз — 50 пудів (на 2 менше), другий раз — 100 пудів (на 5 менше), третій 120 пудів (на 3 менше). Мірошник спочатку додавав «круглі» числа, потім віднімав зазначені числа: 50+100+120-(2+5+3)=260.
1.2 Цікаві факти з історії математики .
Цікаві приклади усного рахунку дійшли до нашого часу. На полотні «Устный счёт. В народной школе С. А. Рачинского» — написаній 1895 році художником Н. П. Богдановим-Бельським ми бачимо урок усного рахунку в сільській школі XIX століття. (Додаток 1).
Учитель — особа цілком реальна, історична. Це математик і ботанік, професор Московського університету Сергій Олександрович Рачинський. Захопившись ідеями народництва в 1872 році Рачинський приїхав з Москви в своє рідне село Татєв і створив там школу з гуртожитком для сільських дітей. Крім того, він розробив власну методику навчання усного рахунку. До речі, художник Богданов-Бєльський і сам був учнем Рачинського. Зверніть увагу на завдання, написане на дошці.
102 + 112 + 122 + 132 + 142
365
102 + 112 + 122 + 132 + 142 = 102 + 122 + 142 + 112 + 132 = 4(52 + 62 + 72) + 112 + (11 + 2)2 = 4(25 + 36 + 49) + 121 + 121 + 44 + 4 = 4 ![]() 110 + 242 + 48 = 440 + 290 = 730.
110 + 242 + 48 = 440 + 290 = 730.
Визначний німецький математик Карл Гаусс (1777-1855) виявив блискучі здібності з математики ще на шкільній парті. Якось на уроці арифметики вчитель запропонував учням додати всі числа від одного до сорока включно. Гаусс майже зразу подав учителеві свою грифельну дошку з правильною відповідю 820. Він звернув увагу на те, що кожна пара чисел, які однаково віддалені від кінців (наприклад, 1+40, 2+39 і т.д.), при додаванні дають те саме число 41, оскільки таких пар 20, то вся сума 41![]() 20=820.
20=820.
Ці приклади показують, що проблема швидких обчислень є актуальною на протязі століть.
РОЗДІЛ 2 СПОСОБИ ШВИДКИХ ОБЧИСЛЕНЬ
2.1 Способи швидкого додавання та віднімання натуральних чисел.
Чи вмієте ви рахувати? Запитання,можливо, образливе для людини старше трьохрічного віку. Хто не вміє рахувати? Та цікава якість цих обчислень.
Розглянемо загальні прийоми усного рахунку.
Наприклад треба додати числа 28, 47, 32 і 13.
а) користуючись десятковим складом числа, розкладемо кожний з доданків на розряди
28=20+8, 32=30+2, 47=40+7, 13=10+3.
б) застосовуючи сполучні і переставні властивості:
(20+30)+(8+2)+(40+10)+(7+3)=50+10+50+10=120.
Розглянемо деякі інші методи.
Правило 1. Якщо один із доданків збільшити на кілька одиниць, то із здобутої суми треба відняти стільки ж одиниць.
364+592 =364+(592+8)-8=364+600-8=964-8=956.
Правило 2. Якщо один із доданків збільшити на кілька одиниць, а другий зменшити на стільки : одиниць, то сума не зміниться.
997+856 = (997+3)+(856-3) = 1000+853 = 1853.
Правило 3. Якщо від’ємник збільшити на кілька одиниць і зменшуване збільшити на стільки ж оди ниць, то різниця не зміниться.
1351 -994 = (1351+6)-(994+6) = 1357-1000 = 357.
Правило 4. Якщо від суми двох чисел відняти різницю цих чисел, то в результаті дістанемо подвоєне менше число, тобто (а+b)-(а-b) = 2b.
(47+24)-(47-24) = 48.
Правило 5. Якщо до суми двох чисел додати їх різницю, то в результаті дістанемо подвоєне більше число, тобто (а+b)+(а-b) = 2а.
(65+34)+(65-34) = 130.
2.2 Окремі методи множення і ділення.
2.2.1 Множення і ділення на 4 і на 8.
Щоб усно помножити число на 4, його двічі подвоюють:
112![]() 4 = 224
4 = 224![]() 2 = 448.
2 = 448.
Щоб усно помножити число на 8, його тричі подвоюють:
117![]() 8 = 234
8 = 234![]() 4 = 468
4 = 468![]() 2 = 936;
2 = 936;
Існують інші прийоми.
Нехай, наприклад, потрібно 28![]() 4. Виконуємо так:
4. Виконуємо так:
а) 28![]() 4=(20+8)
4=(20+8)![]() 4=80+32=112;
4=80+32=112;
б) 28![]() 4=(25+3)
4=(25+3)![]() 4=100+12=112;
4=100+12=112;
в) 28![]() 4=(30-2)
4=(30-2)![]() 4=120-8=112;
4=120-8=112;
г) 28![]() 4=28
4=28![]() 2
2![]() 2=56
2=56![]() 2=112.
2=112.
Нехай треба 128![]() 4, 128=100+20+8, використовуємо розподільний закон множення, множимо 100∙4+20∙4+8∙4=400+80+32=512.
4, 128=100+20+8, використовуємо розподільний закон множення, множимо 100∙4+20∙4+8∙4=400+80+32=512.
Як бачимо можна широко проявляти ініціативу в виборі прийому для виконання даної дії. Таким чином, усний рахунок відкриває широкі можливості для розвитку творчої ініціативи.
Інший спосіб множення на 8 полягає в тому, щоб приписати до першого множника нуль і відняти подвоєний другий множник. Наприклад,
217∙8=2170-434=1736 або 217∙8=200∙8+17∙8=1600+136=1736.
Щоб усно поділити число на 4, його двічі ділять пополам.
Наприклад, 76:4=38:2=19; 256:4=118:2=59.
Щоб усно поділити число на 8, його тричі ділять пополам. Наприклад,
464:8=232:4=116:2=38;
516:8=258:4=129:2=64,5.
2.2.2 Множення на 5 і 25.
Щоб усно помножити число на 5, множать його на 10 і ділять на 2, тобто, приписують числу нуль і ділять його на два. Наприклад:
74∙5=740:2=370;
243∙5=2430:2=1215.
При множені парного числа на 5 зручніше спочатку його поділити на 2, а потім до отриманого результату приписати 0. Наприклад:
74∙5=37∙10=370.
Щоб усно помножити число на 25, множимо його на 100 і поділити на 4,тобто якщо число кратне чотирьом то ділимо на чотири і до результату приписуємо два нулі. Наприклад:
72∙25=18∙100=1800.
Якщо число при ділені на чотири дає остачу, то:
- при остачі 1 до числа приписуємо 25,
- при остачі 2 до числа приписуємо 50,
- при остачі 3 до числа приписуємо 75.
Такий алгоритм виконання обчислень випливає з того, що 100:4=25, 200:4=50, 300:4=75.
2.2.3 Множення чисел за допомогою ліній.
Цікавим є дослідження геометричного методу, в якому множення чисел проводимо за допомогою ліній.
Наприклад:
2![]() 4=8
4=8
Підрахувавши точки перетину отримуємо результат 8.(Додаток 2).
Практично цей метод можна застосувати при множенні двоцифрових та трицифрових чисел.
Наприклад:
15![]() 23=345
23=345
Перетини показують кількість одиниць – 15, 5 одиниць записуємо, а до десятків додаємо 1 десяток, тому 13+1=14 десятків, 4 десятки записуємо, а до сотень додаємо 1, 2+1=3 сотні. Отримуємо добуток – 345.(Додаток 2).
Аналогічно, 123![]() 412=50676. (Додаток 3).
412=50676. (Додаток 3).
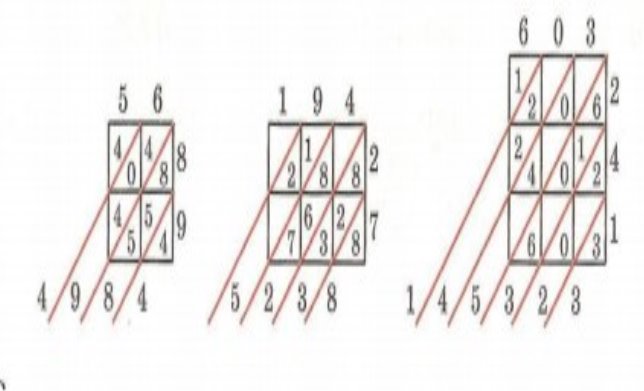
2.2.4 Множення чисел за допомогою алгоритму аль Хорезмі.
Числа записують у вигляді таблиці, кожну клітинку ділимо діагоналлю навпіл. В одній частині записують десятки, а в іншій одиниці добутку відповідних чисел. Для знаходження результату рахують суму чисел, що знаходяться між діагоналями. (Додаток 4 ).
2.2.5 Множення на 9 і 11.
Щоб усно помножити число на 9, дописують до нього нуль і віднімають множник. Наприклад:
62∙9=620-62=558;
73∙9=730-73=657.
Щоб усно помножити число на 11. приписуємо до числа нуль і додаємо множник. Наприклад:
87∙11=870+87=957.
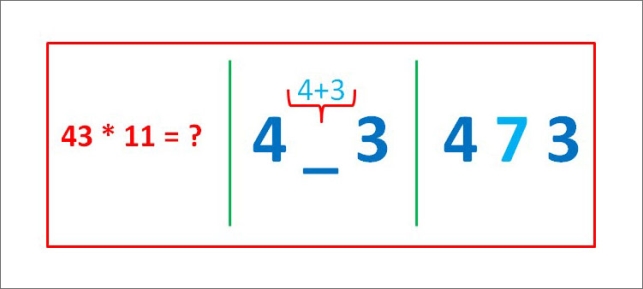
Розглянемо множення чисел на 11 іншими методами, які пропонує Я. Перельман. (Додаток 5).
Записати останню цифру числа, потім послідовно, справа наліво записувати суми сусідніх двох цифр , нарешті, першу цифру.
Наприклад:
43 ![]() 11 = 473
11 = 473
- пишемо 3;
- 4 + 3 = 7, пишемо 7;
- пишемо 4.
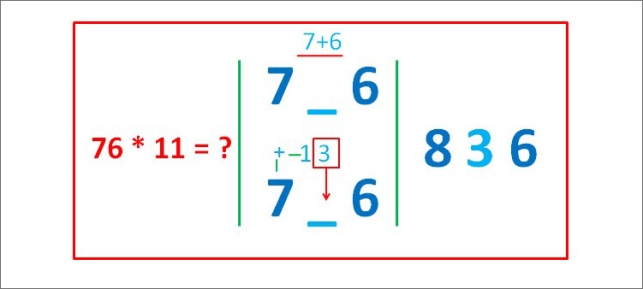
Якщо одна із сум сусідніх цифр виявиться більше 9, то в цьому розряді записують цифру одиниць отриманої суми, а в наступному додають 1.
Наприклад:
76![]() 11=836
11=836
1) пишемо 6,
2) 6 + 7 = 13, пишемо 3 і запам’ятовуємо 1,
3)7 + 1 = 8.
135 ![]() 11 = 1485.
11 = 1485.
- пишемо 5;
- 3 + 5 = 8;
- 1+3=4;
- пишемо 14.
389![]() 11 = 4279
11 = 4279
1) пишемо 9,
2) 8 + 9 = 17, пишемо 7 і запам’ятовуємо 1,
3) 3 + 8 = 11, 11 + 1 = 12, пишемо 2, запам’ятовуємо 1,
4) 3 + 1 = 4.
2.2.6 Множення на одноцифрове та двоцифрове число.
Щоб усно помножити число на однозначний множник, наприклад 27![]() 8, виконуємо такі дії, спочатку перемножуємо десятки (20
8, виконуємо такі дії, спочатку перемножуємо десятки (20![]() 8=160), а потім одиниці (7
8=160), а потім одиниці (7![]() 8=56) і обидва результати додаємо (160+56=216).
8=56) і обидва результати додаємо (160+56=216).
Знаючи цей метод, можна помножити, наприклад, 147∙8 виконавши усно такі дії:
147![]() 8=140
8=140![]() 8+7
8+7![]() 8=1120+56=1176.
8=1120+56=1176.
Коли один із множників розкладається на одноцифрові множники, зручно буває послідовно помножити на ці множники. Наприклад:
225![]() 6=225
6=225![]() 2
2![]() 3=450
3=450![]() 3=1350.
3=1350.
Множення на двоцифрове число можливо виконати наступним чином: коли перший множник одноцифрове число, переставляють множники місцями. Наприклад 6![]() 28=28
28=28![]() 6=20
6=20![]() 6+8
6+8![]() 6=120+48=168.
6=120+48=168.
Якщо обидва множники двоцифрові, то подумки розбивають один із них на десятки і одиниці. Наприклад:
29![]() 12=29
12=29![]() 10+29
10+29![]() 2=290+58=348;
2=290+58=348;
41![]() 16=41
16=41![]() 10+41
10+41![]() 6=410+246=656
6=410+246=656
або
41![]() 16=16
16=16![]() 41=16
41=16![]() 40+16
40+16![]() 1=656.
1=656.
Розбивати на десятки і одиниці вигідно той множник в якого вони виражені меншими числами.
Якщо перший або другий множники легко розкласти усно на однозначні числа, наприклад, 14=2∙7, то користуються цим, щоб зменшити один із множників, збільшивши інший в стільки ж. Наприклад, 45∙14=90∙7=630.
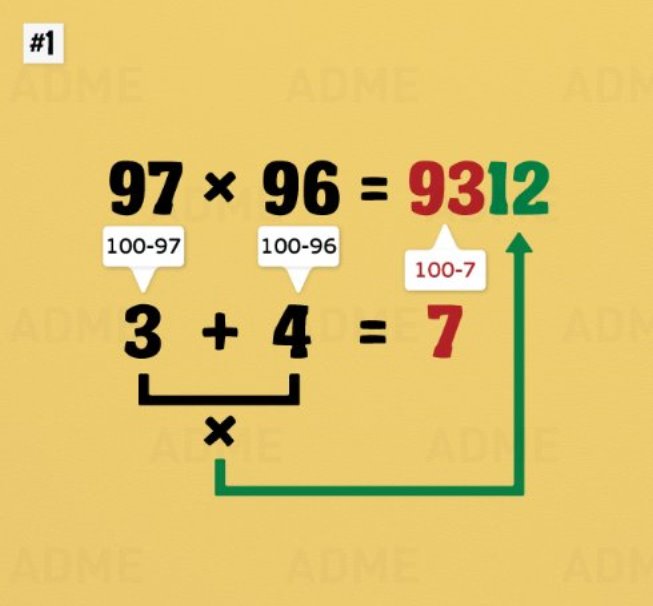
Цікавим є спосіб множення двоцифрових чисел більших за 50, але менших від 100.
Наприклад, 97![]() 96=9312. Необхідно виконати такі дії:
96=9312. Необхідно виконати такі дії:
- 100-97=3;
- 100-97=4;
- 3+4=7;
- 100-7=93;
- 3∙4=12.
Результат четвертої 93 записуємо зліва направо і дописуємо справа 12. Отримуємо відповідь 9312. (Додаток 6).
2.2.7 Піднесення до квадрату чисел, що закінчуються 5.
Щоб піднести до квадрату число яке закінчується цифрою 5 необхідно помножити число десятків на число на 1 більше і приписати 25.
252; 2![]() 3=6; 625;
3=6; 625;
452; 4![]() 5=20; 2025;
5=20; 2025;
1452; 14![]() 15=210; 21025.
15=210; 21025.
Цей спосіб випливає із формули (10х+5)2=100х2+100х+25=100(х+1)+25.
Таким же способом можна підносити до квадрату десяткові дроби, які закінчуються на цифру 5.
8,52=72,25;
14,52=210,25.
2.2.8 Метод додавання та віднімання звичайних дробів «Метелик ».
Для швидкого знаходження результату суми або різниці звичайних дробів можна скористатися таким способом:
- знайти добуток знаменників та чисельників розміщених по діагоналі;
- суму або різницю одержаних добутків записати у чисельнику результату;
- добуток знаменників дробів записати у знаменнику результату.
(Додаток 7).
ВИСНОВКИ
Під час усних обчислень розвиваються такі якості людини, як уважність, зосередженість, витримка, кмітливість, самостійність. Будь-яке обчислення усно можна виконати різними способами.
Нами зроблена спроба дослідити різноманітні методи швидких обчислень, які можуть бути ефективно використані, як на уроках математики, так і в повсякденному житті.
У роботі наведено деякі найпростіші методи обчислень, які легко засвоюватимуться. Більш-менш довгочасне тренування дасть можливість виконувати швидкі усні обчислення з такою безпомилковістю, як і при письмових обчисленнях.
При усному рахунку потрібно пам’ятати самі числа, з якими виконуються дії, деякі проміжні результати, треба пам’ятати деякі найбільш ефективні прийоми усного рахунку. Отже, усний рахунок сприяє тренуванню пам’яті. При усних обчисленнях всім приходиться працювати самостійно і активно.
Звичайно, усно можна порахувати швидше, економніше з точки зору затраченого часу і розумових сил. При цьому важливо те, як виконувалось обчислювання, у чому проявилась творча ініціатива. Отже, усні вправи допомагають математичному розвитку. В усних обчисленнях немає шаблону і прийоми обчислень дуже різноманітні, що також сприяє розвитку людини.
В побуті, на фабриці, на заводі, на ринку приходиться виконувати ті чи інші розрахунки, тому корисно уміти швидко рахувати.
Обчислювачі — віртуози у багатьох випадках полегшують собі роботу, вдаючись до нескладних методів обчислень .
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
- Л. Отдатчикова «Народна математика українців», 2011.
- «Арифметика» Магницького.
http://www.etudes.ru/ru/etudes/magnitskii/
- А. Бадмаев «Некоторые способы быстрых вичислений»
http://www.profistart.ru/ps/blog/2417.html
- Э.Катлер, Р. Мак-Шейн «Система быстрого счета по Трахтенбергу»,«Просвещение»,1967 http://www.mirknig.com/2007/06/20/je.katlerr._makshejjn_._sistema_bystrogo_scheta_po_trakhtenbergu.html
- Я. Перельман. «Быстрый счет. Тридцать простих приемов усного счета».
http://www.likebook.ru/books/view/100455/
- Я.І. Перельман/ Цікава Алгебра. – Київ: Техніка, 1973.
- О.Г Черватюк, Г.Д. Шиманська/ Елементи цікавої математики. – Київ: Радянська школа, 1968.
ДОДАТКИ
Додаток 1

Додаток 2

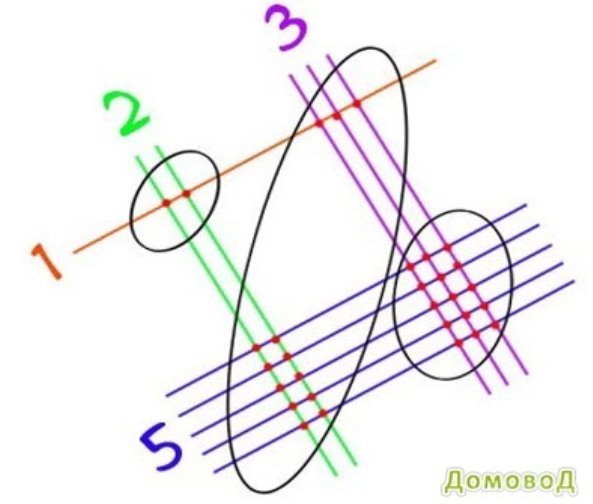
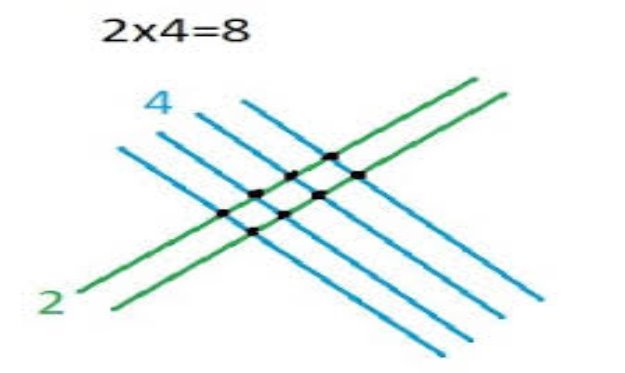
Додаток 3
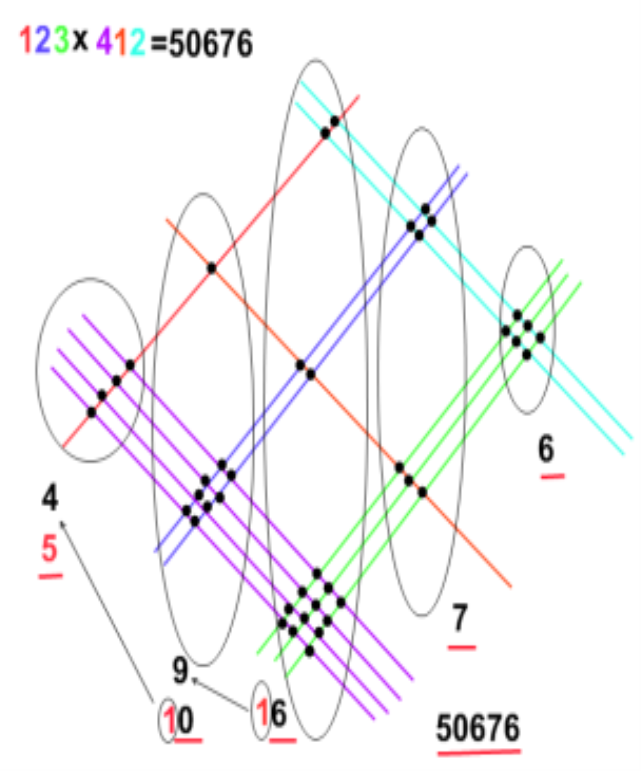
Додаток 4

Додаток 5
Додаток 6
Додаток 7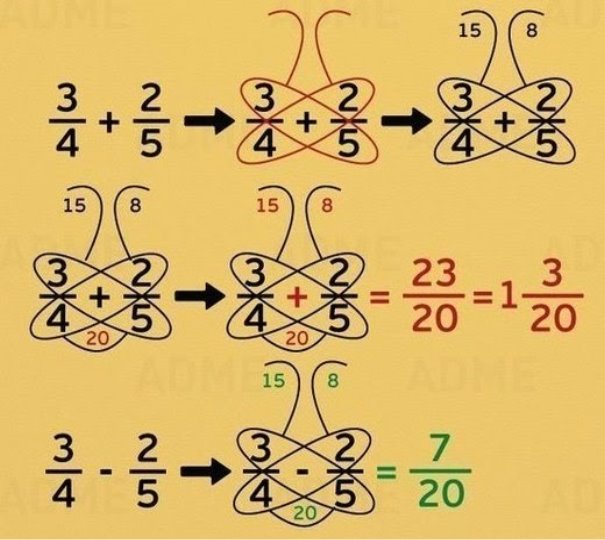
1


про публікацію авторської розробки
Додати розробку
