Тести контрольних робіт з алгебри 11 клас

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Розробила вчителька математики

Пліщинською ЗОШ І-ІІІ ступенів

Ніщук Н.І.

 

 

 

Контрольна работа. Тема: Первісна та інтеграл.

1 Варіант.
1.  (1 бал). Визначити функцію для якої F(x) = x² – sin2x – 1 є первісною:

1) f(x) = ; 

2) f(x) = 2x – 2cos2x;

3)  f(x) = 2x +cos2x; 

4) f(x) = cos2x + x.

2.  (1 бал). Знайти первісну для функції.   F (x) = 4х³ + cos x

1)  F(x) = 12x² – sinx + c;   

2) F(x) = 4x³ + sinx + c; 

3) F(x) = x⁴ – sinx + c;

4)  F(x) = x⁴ + sinx + c.

3.  (1 бал).  Для функції f(x) = х² знайти первісну F, що приймає дане значення в заданій точці   F (- 1) = 2

1)   F(x) = ;     

2)  F(x) = 2x + ;    

3)   F(x) = – ;  

4)  F(x) = .

4. (1 бал). Точка рухається по прямій так, що її швидкість в момент часу t  дорівнює  

V (t) = t + t². Знайти шлях, що пройшла точка за час від 1 до 3 сек., якщо швидкість вимірюється в м /сек.                      

 1)  18 м;          

 2)  12м;          

3)   17м;         

 4)  20 м.

5.   (1 бал). Обчислити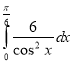                       

 1)  6;       

2)   6;       

3)   2;      

4)    3.

6. (1 бал). Знайти площу криволінійної трапеції, обмеженої лініями  у =  – х² + 3  и  у = 0

1)   4; 

2)   6;        

3)   9;        

4)   8.

7.  (1 бал). Знайти площу фігури, обмеженої лініями  у =   и     у = х

1)  2;            

2)   1;             

 3)   2;             

4)   1.

8.   (1 бал). Обчислити площу фігури, обмеженої графіком функції у = 2 – х², дотичною до цього графіка в його точці з абсцисою х = - 1 і прямою х = 0

1)   1;           

2)   2;            

3)  ;             

4)  1.

9.   (1,5 бали). Обчислити        

10.  (1,5 бали).  Знайти  суму абсцис точок перетину графіків функції у = (х – 1)(х + 2) і її первісної, якщо одна з цих точок знаходится на осі ординат.

11.  (2 бали). Знайти таку первісну функцію  f(x) = 3х – 1 , для якої рівняння  F(x) = 5 має єдиний корінь.

2 Вариант.

1.  (1 бал). Визначити функцію для якої  F(x) = – cos - x³ + 4   є первісною:

1)   f(x) =  - sin - 3x²;   

2)   f(x) = sin - 3x²;

3)  f(x) = - sin - 3x²;  

4)  f(x) = 2sin - 3x² .

2.  (1 бал). Знайти первісну для функції.   f(x) = x² – sinx

  1) F(x) =- cos x + c;

2) F(x) = 2x – cosx + c; 

3)  F(x) = + cosx + c;  

4)  F(x) = + sinx + c

3.  (1 бал).  Для функції  f(x) = 2x – 2 знайти первісну F, що приймає дане значення в заданій точці   А(2;1)

1)   F(x) = - х² – 2х – 1;     

2)  F(x) = х² + 2х + 2;    

3)  F(x) = 2х² – 2;     

4)  F(x) = х² – 2х + 1.

4. (1 бал). Точка рухається по прямій так, що її швидкість в момент часу t  дорівнює  V (t) =3 + 0,2 t.. Знайти шлях, що пройшла точка за час від 1 до 7 сек., якщо швидкість вимірюється в м /сек.                      

1)  22, 8 м;       

2)   29 м;        

3)   23 м;         

4)  13 м.

5.   (1 бал). Обчислити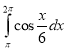         

1)   ;     

2)  3 - 3;      

3)  0;        

4)   3 - 3 .

6. (1 бал). Знайти площу криволінійної трапеції, обмеженої лініями  у =  2х², у = 0, х = 2

1)   5;         

2)     2;         

3)     5;      

4)  2.

7.  (1 бал). Знайти площу фігури, обмеженої лініями  у = 5 – х² ,  у = 1

1)   16;         

2)    5;         

3)   11 ;        

4)   10 .

8.   (1 бал). Обчислити площу фігури, обмеженої графіком функції у = – х² + 3, дотичною до цього графіка в його точці з абсцисою х = 1 і прямою х = 0.

   1)   2;        

 2)   ;        

 3)   2;      

 4)     .

9.   (1,5 бали). Обчислити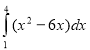         

10.  (1,5 бали).  Знайти  суму абсцис точок перетину графіків функції у = (х – 3)(х + 2) і її первісної, якщо одна з цих точок знаходится на осі ординат.

11.  (2 бали). Знайти таку первісну функцію  f(x) = 2х + 5, для якої  пряма   у = 7х – 3  є дотичною.

 

Контрольна работа. Тема:  Загальне поняття степеня. 

1 Варіант.

 

1. (0,5 балів).  Обчислити:      

1)    14;      

2)   3;        

3)    - 11;       

4) – 11.

2.  (0,5 балів).  Подати вираз у вигляді степеня числа х (х > 0): 

1)  х¹;          

2)  х²;        

3)  х^0,99;      

4)   х^10,9.

3.   (0,5 балів).  Спростити вираз:          

1)  ;        

2)  х⁰;      

3)   ;    

4)    .

4.   (0,5 балів).  Спростити вираз: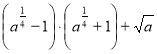 

1)  – 1;       

2)  ;      

3)    а – 1;         

4)  .

5.  (0,5 балів).  Розв’язати рівняння:            

1)  – 4; 3    

2)    – 4;     

3)    3;   

4)  нема коренів.

6.  (1 бал).  Спростити вираз:   , где  а < 0

1)  0;        

2)    ;     

3)   ;   

4)  12а.

7.  (1,5 бали). Обчислити: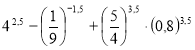   

8.   (1,5 бали). Знайти значення виразу, якщо  m = - 5

      

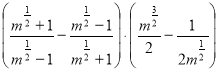
9.  (1,5 бали). Розв’язати систему рівнянь:

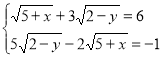         Знайти   у – х, где (х;у) – розв’язок рівняння.

10.  (2 бали).  Розв’язати рівняння: 

11.   (2 бали).  Розв’язати нерівність:  

 

2 Вариант.

1. (0,5 балів).  Обчислити:          

1)   9;     

2)  10- ;      

3) 11;      

4.   9.

2.  (0,5 балів).  Подати вираз у вигляді степеня числа х (х > 0): 

1)   ;      

2)   ;   

3)   х⁰;  

4)  х¹.

3.   (0,5 балів).  Спростити вираз: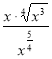           

1)  ;       

2)  х³;    

3)    ;             

4)    .

4.   (0,5 балів).  Спростити вираз: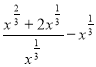          

1)   – 1;      

2)   2х ^{– 1};   

3).    2;    

4).    .

5.  (0,5 балів).  Розв’язати рівняння:       

1)   3;      

2)  1; 3;  

3) – 3;

4)  нема коренів.

6.  (1 бал).  Спростити вираз:  

1)  – 2;     

2)   12 – 4;         

3)  4 - 12;       

4) .

7.  (1,5 бали). Обчислити:    9^1,5 -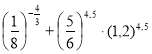  

8.   (1,5 бали). Знайти значення виразу, якщо  а = 16, в = 9

      

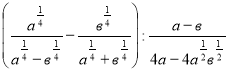
9.  (1,5 бали). Розв’язати систему рівнянь:

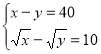         Знайти   у – х, где (х;у) – розв’язок рівняння.

10.  (2 бали).  Розв’язати рівняння: 

 

11.   (2 бали).  Розв’язати нерівність:  

 

Контрольна работа. Тема: Показникова функція.

1 вариант

 

1.  (0,5 балів).  Спростити вираз:

1) 1;         

2) а;         

3) а^2/3;       

4) а^3/2 .

2. (0,5 балів). Вкажіть проміжок, якому належать корені рівняння: 6^3х+1=1/36

1) (-2,25; -1,5);  

2) (-1,5; -0,75);  

3) (-0,75; 0);   

4) коренів нема.

3.  (0,5 балів). Обчислити: (10^-10·100⁶)^-1

 1)  0,0001;      

2) -100;   

3) 0,01;     

4) -10000.

4_.  (0,5 балів). Розв’язати нерівність:  8^3х/5≥0,5

1) (-∞; -5/3];  

2) [-5/3; +∞); 

3)[-5/9; +∞);       

4) (-∞; -5/9].  

5_.  (0,5 балів). Знайти область визначення функції:  у =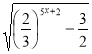

1) (-∞; 0,2);   

2) (-∞; -0,6);   

3) (-∞; 5];    

4)[0,2; +∞);

6_.  (0,5 балів). Графік якої  з перерахованих функцій зображених на рисунку

 

 

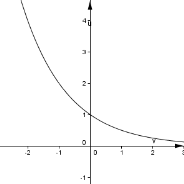
1)  у = (0,5)^х;  

2) у = 2^х;  

3) у = log ₂ х;   

4) у = log _0,5  х.  

7_.  (1 бал).   Знайти добуток  корнів  рівняння  

8.   (1,5 бали).  Решите систему уравнений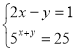            

         Найдите значение х₀+2у₀, где (х_{0 ;} у₀)  - решение системы.

9.  (1,5 бали).  Укажите целое решение неравенства (х - 6)(8^х-6 - 64) < 0 .

10.  (1,5 бали).  Найдите наименьшее значение функции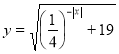

11.  (1,5 бали).  Решите уравнение:   5 · 25^х – (5х - 31)  · 5^х + 6 – х = 0.

12.  (2 бали).  Решите неравенство:    

2 вариант

1.  (0,5 балів).  Обчислити: (4/25) ^-3/2 +0,25

1) 15,875;        

2) 0,186;         

3) 0,01;       

4) 7,75.

2. (0,5 балів). Спростити вираз: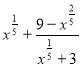           

1) ;        

2) -3;              

3) 9;             

4) 3.

3.  (0,5 балів). Розвязати нерівність: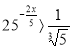

1)       

2)      

3)     

4) 

4_.  (0,5 балів). Вкажіть проміжок, якому належить розвязок рівняння: 8^{х – 1} = 4

 1) ( 0,5 ; 1,25);  

2)  (1,25 ; 1,5 ); 

3)  (1,5 ; 1,75); 

4)  (1,75 ; 2,5).

5_.  (0,5 балів). Знайти область визначення функції:  у =

1)     

2)     

3)       

4)

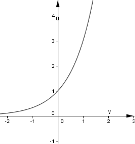
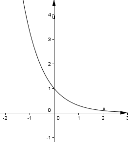
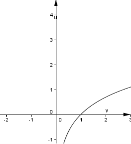
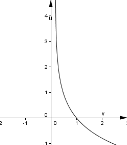6_.  (0,5 балів). _.  На одном з рисунків зображено графік функції 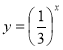.  Вкажіть цей рисунок.

 

 

 

 

 

  1)        2)            3)    4)

 

7_.  (1 бал).   Знайти добуток  корнів  рівняння 2^2х+1 - 7  · 10^х + 5^2х+1 =0

8.   (1,5 бали).  Решите систему уравнений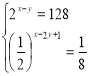            

         Найдите значение 2х₀-у₀,  где (х_{0 ;} у₀)  - решение системы.

9.  (1,5 бали).  Укажите целое решение неравенства (х - 6)(8^х-6 - 64) < 0 .

10.  (1,5 бали).  Найдите наименьшее значение функции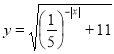

11.  (1,5 бали).  Решите уравнение:   .

12.  (2 бали).  Решите неравенство:    

 

 

:    

Контрольна работа. Тема: Логарифмічна функція.

Логарифмічні рівняння і нерівності.

 

1 Вариант.

1.  (0,5 балів). Знайти значення вирвзу         

1) 6;                

2) 27;             

 3) 12;           

4) 54.

2.  (0,5 балів). Вкажіть проміжок, якому належить розв’язок рівняння:    

1)  (-3;  1);         

2) (- ; -3);            

3)  (4;  +);            

4)  ( 2;  4 ).

3.  (0,5 балів).  Знайдіть область визначення виразу:  

1) ;      

2) ;            

3) ;         

 4)

4.  (0,5 балів).  Знайдіть значення виразу:    log₃(9b),   если   log₃b = 5.

1)  25;         

2)  10;         

3) -8;          

4) 7.

5.  (0,5 балів). Розв’язати нерівність:    log₂( 1 – 0,3)4.

1) ;        

 2) ;           

3) ;        

4)

6. (1 бал). Вказати наименьше ціле число з області визначення  функції 

7.  (1 бал). Знайдіть добуток коренів рівняння    .

8.  (1 бал). Знайти значення виразу    

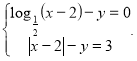9. (1,5 бали).  Нехай  - розв’язок системи рівнянь     Знайти суму  

10.  (1,5 бали).  Розв’язати рівняння   

11.  (1,5 бали).  Розв’язати нерівність   

12.  (2 бали). Знайти значення , при яких область визначення  функції        містить рівно три цілих числа.

2 Вариант.

1.  (0,5 балів). Знайти значення вирвзу                                                                                               1)  1;         

 2) -9;            

3)  3;             

4) -1,5.

2.  (0,5 балів). Вкажіть проміжок, якому належить розв’язок рівняння:     .

1) ( -4;  -2);        

2) ( 6;  8);             

3) ( 3;  6);              

4) ( -8; -6).

3.  (0,5 балів).  Знайдіть область визначення виразу:   y = log_0,1(0,01 –).  

1)     

2);   

3)       

4)

4.  (0,5 балів).  Знайдіть значення виразу:    , якщо    .          

1)  1;             

2) -7;         

3)  -1;           

 4) 7.

5.  (0,5 балів). Розв’язати нерівність:   

1)    

 2)  

3)

4)

6. (1 бал). Знайти  наименьше значення  функції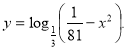 

7.  (1 бал). Знайти цілий розвязок нерівності 

8.  (1 бал). Знайти значення виразу    

9. (1,5 бали).  Нехай  - розв’язок системи рівнянь 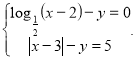    Знайти суму  

10.  (1,5 бали).  Розв’язати рівняння   

11.  (1,5 бали).  Розв’язати нерівність   

12.  (2 бали). Знайти всі додатні, не рівні 1, значення , при яких область визначення  функції     не містить двохзначних натуральних чисел.