УРОК (Алгебра 11 клас) "Інтеграл та його застосування"
УРОК (Алгебра 11 клас) - нестандартний
Інтеграл та його застосування.
Мета уроку: удосконалити вміння учнів використовувати формулу для обчислення об’ємів тіл обертання; показати застосування цієї формули для обчислення об’ємів кулі, конуса, циліндра; можливість застосування інтеграла в різних галузях фізики, економіки й техніки;
підготовити учнів до контрольної роботи; розвивати самостійність, уміння працювати в групі, працьовитість, наполегливість, відповідальність.
Тип уроку: застосування знань, умінь і навичок
Організаційний етап.
Учні заздалегідь об’єднуються в групи (практиків (3 групи), фізиків і економістів). Кожна група складається з п’яти учнів.
Перевірка домашнього завдання.
На дошці подано розв’язок завдань, учні взаємоперевіркою виправляють помилки. В кінці уроку здають зошити на перевірку. Троє учнів відновлюють розв’язання вибіркових завдань.
Розв’язання завдань рівня В:
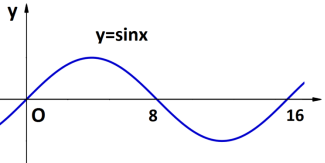
1. 1) На проміжку [0;8] швидкість
додатна і точка рухається в одному
напрямку, а на проміжку [8;16]
швидкість від’ємна і в момент t=16 c.
точка повернеться в початкове
положення, тобто переміщення
дорівнює нулю.
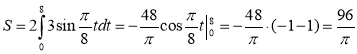
2) (м)
2.1) 2)
Актуалізація опорних знань.
Вправа «Втрачена інформація»
У тексті пропущені слова, які учні вписують, а потім здійснюють взаємоперевірку між групами з подальшим зчитуванням правильних відповідей. (Кожне питання – 0,25 б.)
1. Формула Ньютона — Лейбніца: … , де F(x)-….
2. Задачі, у яких використовуються нематематичні поняття, називають...
3. Рівняння x2 + y2 = R2 задає ... із центром ..., де R — ...
4. Пряма, яка проходить через початок координат, задається рівнянням
y =...
5. Пряма, паралельна осі Ox, задається рівнянням y =...
6. Шлях, пройдений тілом за інтервал часу [t1 ; t2], виражається
через інтеграл так: s = ...
7. Роботу змінної сили F(x) під час переміщення тіла із точки a
в точку b можна знайти за формулою A = ...
8. Електричний заряд, що проходить через поперечний переріз провідника за проміжок часу від t1 до t2, можна знайти за
формулою q = ...
Удосконалення вмінь і навичок.
За тиждень до уроку групи отримали завдання знайти матеріал,
на прикладі якого можна продемонструвати застосування інтеграла при обчисленні об’ємів кулі, циліндра, конуса, застосування інтеграла при розв’язанні задач з фізики та економіки.
Група «практиків»
Три групи практиків працюють над розв’язанням задач на обчислення: об’єму кулі; об’єму циліндра; об’єму конуса з подальшим поясненням біля дошки.
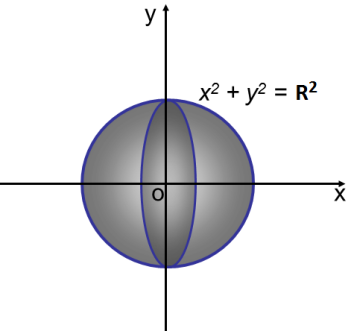
1. Об’єм кулі.
x2 + y2 = R2, y2 = R2 − x2. Якщо y > 0,
то
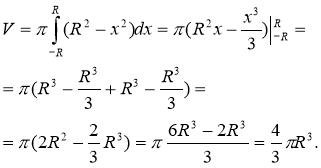
Таким чином, Vк.= (5 б.)
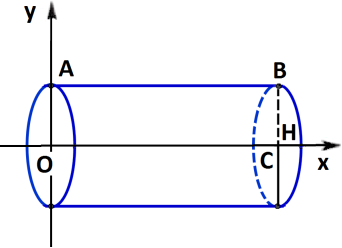
2. Об’єм циліндра.
Циліндр — тіло, отримане
обертанням прямокутника OABC
навколо осі Ox.
Складемо рівняння твірної
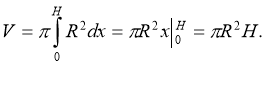циліндра AB: y = R.
Vц.=R2H (5 б.)
Об’єм конуса.
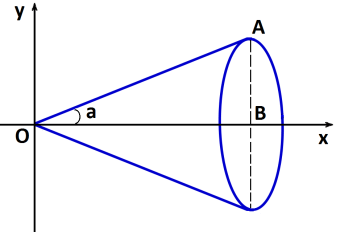Трикутник OAB обертається
навколо осі Ox. Складемо рівняння
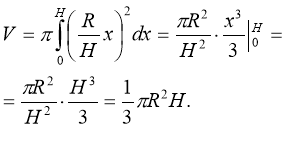твірної конуса OA: y = kx, де k=tga=
.
Таким чином, Vкон.= 
R2H. (5 б.)
Група «фізиків»
Група «фізиків» працює над розв’язанням задачі з фізики з подальшим поясненням біля дошки.
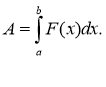Задача. Робота сили F(x) під час переміщення тіла із точки a в точку b дорівнює
Обчисліть роботу, яку треба виконати для викачування води з ями завглибшки 10 м, яка має квадратний переріз зі стороною 4 м. Густина води ρ = 103 кг/м3.
Розв’язання: Напрямимо вісь Ox уздовж діючої сили F(x).
Сила F(x), яка діє на переріз прямокутного паралелепіпеда площею
16 м2 , дорівнює вазі шару води, що перебуває над цим перерізом.
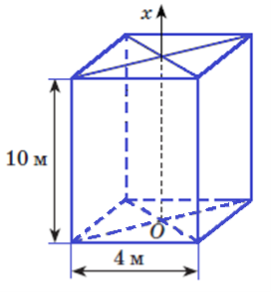Тоді F(x) = 16ρg (10 − x), де x ∈[0;10]; g = 9,8 м/с2 .
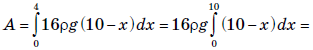
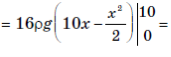
(5 б.)
Група «економістів»
Група «економістів» працює над розв’язанням задачі економічного
змісту з подальшим поясненням біля дошки.
Задача. Продуктивність праці робітника приблизно виражається
формулою f (t) = −0,0033t2 −0,089t +20,96 , де t — робочий час
(у годинах). Обчисліть обсяг випуску продукції за квартал, вважаючи, що робочий день триває 8 годин, а кількість робочих днів у кварталі – 62.
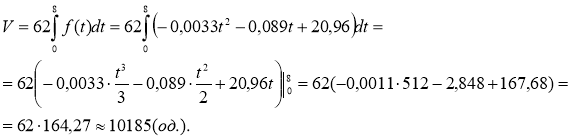Розв’язання: Об’єм випуску продукції протягом зміни є первісною від функції, що виражає продуктивність праці. Тому протягом кварталу обсяг випуску продукції становитиме:
Повторення та систематизація вмінь.
Розв’яжіть кросворд
1. Першу букву якого слова нагадує знак інтеграла? (Summa - сума)
2. Хто із відомих математиків-фізиків розглянув фізичний зміст інтеграла? (Ньютон)
3. Хто із відомих математиків розглянув математичний зміст інтеграла? (Лейбніц)
4. Як називається трапеція, площу якої ми знаходимо за допомогою визначеного інтеграла? (Криволінійна)
5. Як називається функція, яка стоїть пі знаком інтеграла? (Підінтегральна)
6. Як називається множник dx в
підінтегральному виразі?
(Диференціал)
7. Як називається операція
обернена до операції
диференціювання?
(Інтегрування)
Якщо учні правильно відповіли
на всі запитання, то вони одержать слово
«Молодці». (Кожне питання – 0,5 б)
Вправа «Дешифрувальник»
Виконайте завдання і знайдіть ім’я вченого, якому належить таке висловлювання:
«Теория без практики мертва или бесплодна:
практика без теории невозможна или пагубна.
Для теории нужны знания, для практики, сверх того и умение».
Декарт
Заповніть таблицю:
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
|
Буква |
|
|
|
|
|
|
1. Знайдіть загальний вигляд первісної для функції f(x)=4e2x+1. (1 б.)
|
Б |
В |
Г |
Д |
|
8е2х+1 + С |
4е2х+1 + С |
8е2х+1 + С |
2е2х+1 + С |
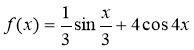
2. Знайдіть первісну функції , графік якої проходить через точку А (; 3). (2 б.)
|
Е |
|
З |
|
|
|
|
|
|
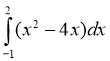
3. Обчисліть: (1 б.)
|
З |
K |
Л |
М |
|
-3 |
-3 |
-7 |
-7 |
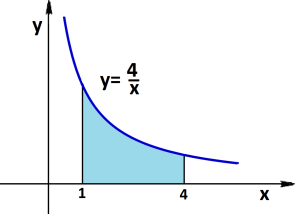
4. Обчисліть площу зафарбованої
фігури, зображеної на рисунку
(1 б.)
|
І |
О |
|
4ln4 - 4 |
ln4 |
|
|
|
|
А |
У |
|
4ln4 |
4ln3 |
5. Обчисліть площу фігури, обмеженої лініями:
у=-x2+8 i y=4. (2 б.)
|
Р |
С |
Т |
Ф |
|
|
32 |
|
16 |
6. Знайдіть об’єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої кривою у=х3 і прямими х=1 і х=2. (2 б.)
|
Д |
С |
Г |
Т |
|
127 |
127 |
|
|
До завдань 2, 5, 6 складіть план розв’язання задачі.
По закінченні відбувається обов’язкове обговорення складених планів.
Самостійна робота (завдання на вибір).
Аукціон задач
Картка-завдання «Логікус»
1.Обчисліть інтеграли:
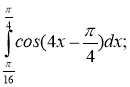
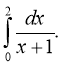
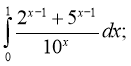
2.Знайдіть площу плоскої фігури, обмеженої прямою у=4, параболою у=3х2-10х+7 і дотичною до цієї параболи, проведеною через точку з абсцисою х0=2.
(Кожне завдання – 3 б.)
Картка-завдання «Ерудит»
-
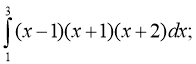
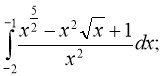
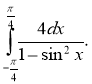Обчислити інтеграли:
2. Знайдіть площу фігури, обмеженої лініями: у=-х2+2х+10, у=10.
(Кожне завдання – 2 б.)
Картка-завдання «Кмітливий»
-
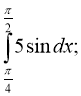Обчислити інтеграли:
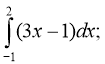
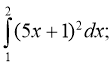
- Обчислити площу плоскої фігури, обмеженої параболою у=1-х2 і віссю Ох.
(Кожне завдання – 1 б.)
Підбиття підсумків уроку.
Оціночний лист учня
|
Завдання |
Домашня робота |
«Втрачена інформація» |
Домашнє завдання групи |
Кросворд |
«Дешифру-вальник» |
Аукціон задач |
Додаткові бали |
Всього: |
|
Отримані бали |
|
|
|
|
|
|
|
|
Домашнє завдання
Підготуватися до контрольної роботи: повторити теоретичний матеріал (опорні конспекти з теми «Інтеграл»),
Умова домашньої контрольної роботи.
1. Для функції f(x)=cosx знайдіть первісну, графік якої проходить через точку А .
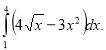2. Знайдіть .
3. Обчисліть інтеграл
4. Тіло рухається прямолінійно зі швидкістю ʋ(t)=t+3t2(м/с).
Знайдіть шлях, пройдений тілом за проміжок часу від t=1 с. до t=2 с.
5.Обчисліть площу фігури, обмеженої лініями у=4х-х2, у=4-х.
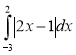
Додатково:
Рефлексія
|
Як ви вважаєте працювала група? |
дружно всі |
|
не всі активні |
|
вяло, багато помилок |
|
|
Якого життєвого досвіду ви набули? |
володіти собой |
|
захищати свої нання |
|
бути впевненим в собі |
|
|
Чи вичерпали ви свої можливості? |
|
|||||
|
Під час підготовки до контрольної роботи мені слід звернути увагу? |
|
|||||
про публікацію авторської розробки
Додати розробку