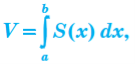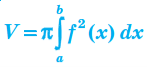УРОК (Алгебра 11 клас) "Застосування інтеграла до обчислення площ і об’ємів"

УРОК  (Алгебра 11 клас)

Застосування інтеграла до обчислення площ і об’ємів.

Мета уроку: закріпити знання учнів з обчислення табличних інтегралів, застосування властивостей визначеного інтеграла, продовжити формування вмінь учнів обчислювати площі плоских фігур, розпочати формування вмінь учнів застосовувати визначений

інтеграл до обчислення об’ємів тіл; розвивати абстрактне та логічне мислення, уявлення про тривимірну просторову будову тіл, уміння спостерігати, аналізувати та обчислювати, робити висновки, сприяти розвитку інтересу до вивчення математики; охайність, математичну культуру, вміння підпорядковувати свої дії загальній справі, планувати свої дії, виявляти практичну спрямованість навчального матеріалу.

 

Перевірка домашнього завдання.

На дошці подано розв’язок завдань, учні взаємоперевіркою виправляють помилки. Троє учнів відновлюють розв’язання вибіркових завдань.

 

Актуалізація опорних знань.

Інтерактивна вправа «Мікрофон».

1. Сформулюйте означення первісної функції.                          

2. Заповніть таблицю первісних функцій (Дані функції проектуються на екран).                                                                                                 

3. Як називається операція знаходження первісної?

4. Наведіть означення криволінійної трапеції.

5. Сформулюйте означення визначеного інтеграла.

6. Який геометричний зміст визначеного інтеграла?

7. Запишіть формулу Ньютона-Лейбніца.

8. Сформулюйте чотири основні властивості визначеного інтеграла

9. Як обчислити за допомогою визначеного інтеграла площу плоскої фігури? (Приклади різного розміщення фігур проектуються на екран).

10. Подайте у вигляді многочлена:

     1) (х²-2х)²;  2) (х+х²)²;  3) (2-х²)².

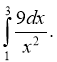
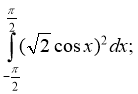11. Обчисліть інтеграл:

     

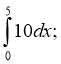
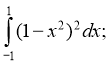
   1)           2)               3)                      4)                           5)

 

12. Що таке об’єм геометричного тіла?

13. Сформулюйте властивості об’єму геометричних тіл.

 

 

Створення відповідної мотивації до вивчення нового матеріалу.

Проблемне завдання

 

Завдання. Обчислити об’єм яблука, яке має неправильну форму.

Використати яку-небудь відому формулу для обчислення

об’єму неможливо. Можливо, учні здогадаються (за аналогією з обчисленням площі криволінійної трапеції), що яблуко слід розрізати на тоненькі скибочки, кожну з яких можна вважати циліндром, виміряти радіус кожного циліндра й обчислити об’єм за відомою формулою.

Після заслуховування пропозицій, які вискажуть учні, повідомляємо, що існує спосіб застосування інтеграла до обчислення об’ємів тіл.

Засвоєння нових знань.

 

Опорний конспект №7

Об’єми тіл

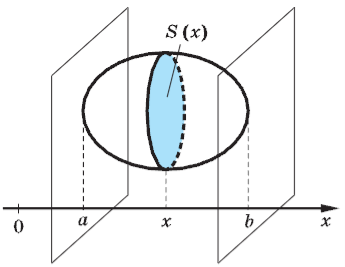
1. Застосування визначеного інтеграла до обчислення об’єму будь-якого тіла Якщо тіло вміщене між двома перпендикулярними до осі Ox площинами, що проходять через точки x = a і x = b, то                             де S(x) — площа перерізу тіла площиною, що проходить через точку x ∈[a;b] і перпендикулярна до осі Ox.   2. 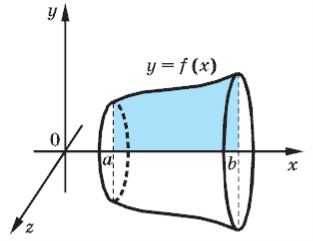Застосування визначеного інтеграла до обчислення об’єму тіла, одержаного в результаті обертання криволінійної трапеції навколо осі Ox Якщо тіло одержане в результаті обертання навколо осі Ox криволінійної трапеції, яка обмежена графіком неперервної і невід’ємної на відрізку [a;b] функції y = f (x) і прямими x = a і x = b, то

 

 

 

 

 

 

 

 

Розв’язуємо разом

 

Приклад 1. Обчисліть об’єм тіла, утвореного обертанням навколо

осі абсцис фігури, обмеженої лініями y = 4 − x² та y = 0.

 

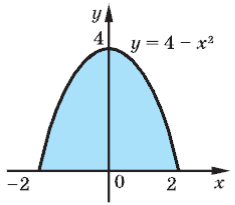Розв’язання. Зобразимо задану фігуру і

переконаємося, що вона є

криволінійною трапецією.

У цьому випадку об’єм тіла обертання

можна обчислити за формулою

 

 

 

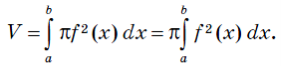
Щоб визначити межі інтегрування, знайдемо абсциси точок перетину заданих ліній.

4 − x² = 0, x₁ = −2, x₂ = 2.

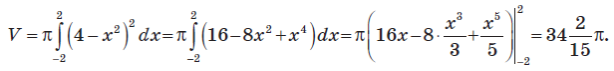Тоді

 

 

 

 

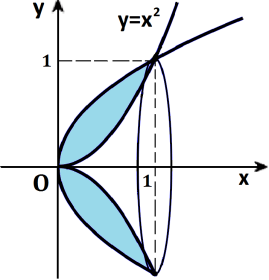
Приклад 2. Фігура, обмежена параболами

у=х² та у=, обертається навколо осі абсцис.                              у=

Обчисліть об’єм тіла, утвореного в результаті                            

обертання цієї фігури.

 

Розв’язання. Знаходимо межі інтегрування:

        у=х²

        у=,       х⁴ = х,  х(х³-1) = 0,

                       х(х -1)(х²+х+1)=0,

                       х₁=0,  х₂=1.                  

                                  

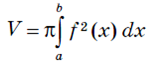
 Застосуємо формулу                           ,

 

маємо:

                                                                                    

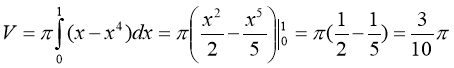
                                                                                     (куб. од.).                                                                                                        

 

 

 

 

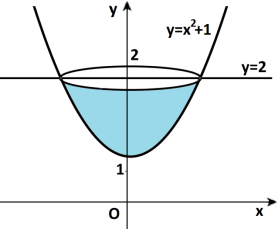
Приклад 3. Обчисліть об’єм тіла, утвореного обертанням навколо осі Оу фігури, обмеженої параболою у=х²+1 і прямою у=2.

 

Розв’язання. Об’єм утвореного тіла (воно називається параболоїдом) обчислюємо за формулою:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

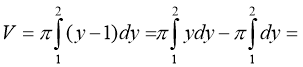
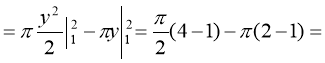
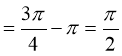
               (куб. од.).

 

Удосконалення знань і умінь.

 

Дидактична гра

Учні об’єднуються у команди.

Ігрове поле складається з розмальованого планшета, на якому зображено гору з нанесеним на неї маршрутом сходження на зупинки. Зупинки пронумеровані, старт позначено прапорцем.

Команди з головуючим займають старт – початкову позицію. На кожній зупинці викладач перевіряє правильність виконання завдання. Виграє та команда, яка підніметься на «вершину знань».

 

1. Розщілина «Графічна».

 

Картка - завдання

Знайдіть первісні функцій, що задовольняють дану умову:

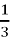1. f(x) = cos + 4cos4x, F()=3;                                              (1,5 б.)
2. f(x) = 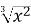+ 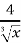, F(1)=0;                                                         (1,5 б.)
3. f(x) = 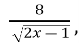F(0,5)=7;                                                           (1,5 б.)
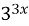4. f(x) = – 5∙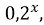 F(0)=0                                                    (1,5 б.)

 Для функції f (x) знайдіть первісну, графік якої проходить через

 точку А, якщо:                                                                              (2 б.)

 

  5)                                т. А(;0)                                                      

 

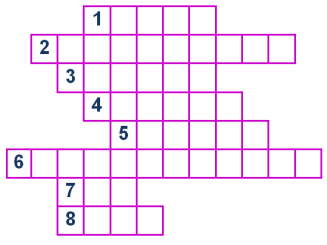
2. Гірський хребет  «Інтеграла».

 

            Розв’яжіть кросворд

 

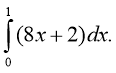           Завдання:

 

1.                          (1 б.) 

 

 

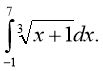
    2.                         (1 б.)

 

 

 

 

 

 

 

 

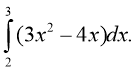
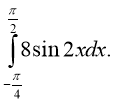
3.                            (1 б.)                  4.                              (1 б.)

 

                       

 

 

5. Множина всіх точок координатної площини з координатами (х; f(x)), де перша координата набуває всіх значень з області визначення функції у= f(x), а друга координата – це відповідні значення функції в точці х.                                                                                             (1 б.)

 

 

 

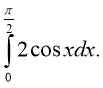
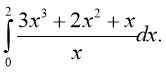
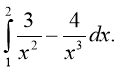
6.                                     7.                           8.                                 (1 б.)

 

 

 

 

3. Плато «Криволінійна трапеція».

 

Картка - завдання

 

Обчислити площу фігури, обмеженої лініями:

 

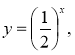
1)               у=0, х=-3, х=2;   (1 б.)      2)  у=,  у=0, х=5;             (1 б.)

 

 

3)             х+у=6;   (1 б.)       4) у=cosx,  x=0,  x= та віссю абсцис.   (1 б.)

 

5) у=sinx, у=х²-х    (3 б.)

 

4. Вершина «Об’ємного успіху».

 

Картка - завдання

 

Знайти об’єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої:

1) графіком функції у=4х та прямими х=9, у=0;                     (1 б.)

2) косинусоїдою у=сosx та прямими х=0, х=, у=0;                 (1 б.)

3) прямими у=2х, х=0, у=5;                                                      (1 б.)

4) кривою у=х³ і прямими х=1 і х=2.                                        (1 б.)

5) у²-4х=0, х-2=0, х-4=0, у=0                                                     (2 б.)

 

Викладач оголошує результати дидактичної гри.

Хто дійшов до десятитисячної вершини «Об’ємного успіху», той одержує знак «Майстер математичного альпінізму».

 

 

 

 

Історична довідка

Ідеї інтегрального числення зустрічаються ще у працях стародавніх математиків. Про це свідчить «метод вичерпування» Евдокса, який пізніше використав Архімед у ІІІ ст. до н.є. Суть цього метода полягає в тому, що для обчислення площі плоскої фігури (об’єму тіла) навколо них описували і в них вписували ступінчасті фігури і, збільшуючи кількість сторін многокутника (граней многогранника), знаходили границю, до якої прямували площі (об’єми) ступінчастих фігур. Але проблема загального методу обчислення площ і об’ємів фігур залишалася нерозв’язаною.

До історії математики увійшов так званий принцип Кавальєрі італійського математика Бонавентуро Кавальєрі (1598-1647), за допомогою якого обчислювали площі та об’єми. Для площ плоских фігур принцип Кавальєрі формулювали так, якщо прямі деякого пучка паралельних прямих перетинають фігури Ф₁ і Ф₂ по відрізках однакової довжини, то площі фігур Ф₁ і Ф₂ рівні.

Ідеї Кавальєрі та інших учених стали тим ґрунтом, на якому І. Ньютон і Г. Лейбніц відкрили інтегральне числення. Сучасне означення інтеграла як границі інтегральних сум належить О. Коші. Символ      був введений Г. Лейбніцем.

Знак    нагадує розтягнуту букву літеру S. Термін «інтеграл» проходить від латинського слова integer – «цілий» і був запропонований у 1690 р. Й. Бернуллі.

У галузі інтегрального числення плідно працював український математик

М. В. Остроградський.

Підбиття підсумків уроку.

Капітани оцінюють роботу учнів на уроці за кількістю зароблених ними балів. Кожен учень виставляє отримані бали в облікову відомість. На уроці за відповіді, активну роботу в команді, виступи при обговоренні питань, роботу біля дошки тощо учні отримують додаткові бали.

Оціночний лист учня

Завдання	Домашня робота	«Мікрофон»	Розщілина «Графічна»	Кросворд	Плато «Криволінійна трапеція»	Вершина «Об’ємного успіху»	Додаткові бали	Всього:
Отримані бали

Контрольне запитання

Поясніть, як можна обчислити об’єм тіла за допомогою визначеного інтеграла. Наведіть приклади.

 

Домашнє завдання.

Вивчити теоретичний матеріал (опорний конспект №7), п.27 (опрацювати)

підручник А.Г. Мерзляк, Д.А. Номіровський,   В.Б. Полонський, М.С. Якір  Алгебра 11 класс. Завдання: № 27.2.

 Додатково: Обчислити площу плоскої фігури, обмеженої графіками функцій

у=-х² – 2х + 8, у=х² + 2х +2 (Д); Обчислити площу плоскої фігури, обмеженої графіками функцій: 1) у = (х+1)² і у=4-х; 2) гіперболою у=, дотичною до неї, проведеною в точці з абсцисою х=1, і прямою х=2 (В).

Рефлексія

Порівняйте свої знання на початку уроку і в кінці?
Найпростішим для мене було завдання?
Найскладнішим виявилось завдання?
Розвитку яких рис характеру сприяв урок (само-стійності, спостережливості, відповідальності)?
Чи отримали ви задоволення від власної праці?