Урок для 6 класу ,,Поділ числа у даному відношенні,,

Тема уроку: Поділ числа у даному відношенні.

Мета уроку:Формувати вміння учнів використовувати властивості пропорцій до розв’язування задач на пропорційний поділ та задач логічного характеру. Використовувати міжпредметні зв’язки для формування в учнів цілісного уявлення про систему знань, розвивати вміння аналізувати ситуацію з різних боків, творчі здібності, гнучкість мислення.Виховувати культуру математичного мовлення, математичних записів.

Тип уроку: Формування навичок і вмінь, узагальнення та систематизація знань.

Дата:

Клас: 6-

                                                    Хід уроку

І Актуалізація опорних знань.Перевірка домашнього завдання.

1. Що називається пропорцією?
2. Як називаються члени пропорції?
3. Назвіть основну властивість пропорції.
4. Які величини називають прямо пропорційними?
5. Назвіть властивість прямо пропорційних величин.

Проводиться взаємоперевірка учнями домашнього завдання.

ІІ Вивчення нового матеріалу.

   Пропорційність має широке застосування в мистецтві, архітектурі, живописі, скульптурі. Вона означає додержання певних співвідношень між окремими ча­стинами споруди, картини, скульптурного твору, що справляє найприємніше враження. Архітектуру часто називають «завмерлою музикою». Стародавні греки учення про відношення та пропорції називали музикою, яку вважали га­луззю математики. Художник, скульптор, архітектор, музикант, інженер-усі во­ни ознайомлені з пропорцією та її властивостями.

Розглянемо задачі, в яких вимагається поділити число або значення величини у даному відношенні, тобто на частини, пропорційні деяким числам. Такі задачі називають задачами на поділ числа у даному відношенні або задачами на пропорційний поділ.

Задача 1. Сплав масою 30 кг складається із заліза і міді, які взято у відношенні 3 : 2. Скільки у сплаві заліза і скільки міді?

 Розв’язання. І спосіб. (Мал. 8). Маси заліза і міді відносяться як 3 : 2, тобто до сплаву входить 3 частини заліза і 2 частини міді. Всього маємо 3 + 2 = 5 (частин). Оскільки п’яти частинам відповідає 30 кг, то на одну частину припадає 30 : 5 = 6 (кг). Тоді заліза у сплаві 6 ∙ 3 = 18 (кг), а міді 6∙ 2 = 12 (кг).

Мал. 8

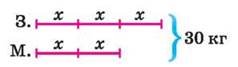
Мал. 9

II спосіб. (Мал. 9). Позначимо масу однієї частини буквою х. Оскільки заліза взято три частини, то його у сплаві х + х + х = 3х (кг), а міді взято дві частини, тому її у сплаві х + х = 2х (кг).

За умовою маємо рівняння 3х + 2х = 30. Тоді 5х = 30. Отже, х = 6 (кг) — маса однієї частини, тобто 6 ∙ 3 = 18 (кг) — взято заліза, 6 ∙ 2 = 12 (кг) — міді.

Відповідь. 18 кг заліза і 12 кг міді.

Часто число або значення величини необхідно поділити на три і біль- ше частин. Так, наприклад, якщо число треба поділити на три частини, пропорційно числам 2, 3 і 4, то кажуть, що число треба поділити у відношенні 2 : 3 : 4; якщо відрізок треба поділити пропорційно числам 3, 7, 5 і 1, то кажуть, що відрізок треба поділити у відношенні 3 : 7 : 5 : 1.

Задача 2. Між мамою, татом і їхнім сином поділили яблука у відношенні 2 : 1 : 3. Скільки яблук отримала мама і скільки тато, якщо син отримав 12 яблук?

Розв’язання. Оскільки трьом частинам відповідають 12 яблук, то на одну частину припадає 12 : 3 = 4 (яблука). Отже, тато отримав 4 яблука, а мама — 4 ∙ 2 = 8 (яблук).

Відповідь. 4 яблука — тато, 8 яблук — мама.

ІІІ Закріплення знань.Розв’язування вправ.

Ст. 116,№ 622,№ 624,№626,№627,№628.

№ 622. Поділи:

1)     число 21 на дві частини у відношенні 2 : 5;

Нехай х-одна частина.Шукані числа будуть дорівнювати 2х і 5х.

Складемо рівняння та  знайдемо х:

2х+5х=21

7х=21

Х=21:7

Х=3,

Тоді шукні числа:

2х=2*3=6

5х=5*3=15

Відповідь: 6 і 15.

2)     число 48 на три частини у відношенні 3 : 7 : 2.

Нехай х-одна частина.Шукані числа будуть дорівнювати 3х,7х і 2х.

Складемо рівняння та  знайдемо х:

3х+7х+2х=48

12х=48

х=48:12

х=4,

тоді шукані числа:

3х=3*4=12

7х=7*3=21

2х=2*3=6

Відповідь: 12;21;6.

№ 624.  Латунь — це сплав міді і цинку, маси яких відносяться як 3 : 2. Для виготовлення шматка латуні потрібно 240 г міді. Скільки треба взяти цинку, щоб виплавити такий шматок латуні?

Мідь	+	Цинк	=	Латунь
3х		2х
240г		?

Нехай х-одна частина,тоді-для виготовлення латуні потрібно 3х міді та 2х цинку.

Складемо табличку з відомими значеннями.Знайдемо х:

3х=240

Х=240:3

Х=80-одна частина

Знайдемо скільки потрібно цинку:

2х=2*80=160(г)

Відповідь: 160г.

№ 626.  Для виготовлення соку беруть 3  частини фруктів і 5 частин води. Скільки фруктів треба взяти, щоб отримати 96 кг соку?

Нехай х-одна частина,тоді для виготовлення соку потрібно 3х фруктів та 5х води.Складемо рівняння та знайдемо х:

3х+5х=96

8х=96

Х=96:8

Х=12

Тоді:3х=3*12=36(кг)

5х=5*12=60 (кг)

Відповідь:36 кг фруктів,60 кг води.

 

№ 627. Периметр трикутника дорівнює 60 дм, а довжини сторін відносяться як 6 : 5 : 4. Знайди сторони трикутника.

Нехай х-одна частина,тоді сторони трикутника дорівнюють-6х,5х та 4х.

Складемо рівняння:6х+5х+4х=60

15х=60

Х=60:15

Х=4

Тоді шукані сторони дорівнюють: 6х=6*4=24(дм)

5х=5*4=20(дм)

4х=4*4=16 (дм)

Відповідь: 24дм;20дм;16дм.

№ 629.  Сторони трикутника відносяться як 2 : 3 : 4. Різниця найбільшої і найменшої сторін дорівнює 12 см. Знайди сторони трикутника.

Нехай х-одна частина,тоді шукані сторони трикутника дорівнюють:2х,3х,4х.

За відомим співвідношенням складемо рівняння: 4х-2х=12

2х=12

Х=12:2

Х=6

Тоді довжини сторін трикутника дорівнюють: 2х=2*6=12(см)

3х=3*6=18 (см)

4х=4*6=24 (см)

Відповідь:12см,18см,24см.

ІV Підсумок уроку.

V Домашнє завдання

§24,№623,№629,№ 634.