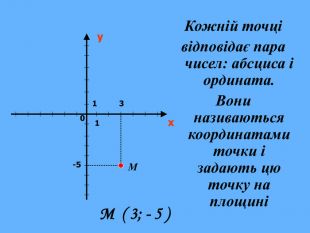
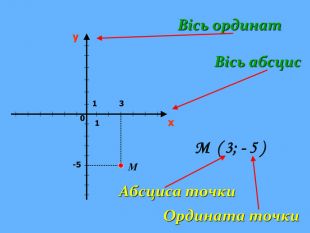
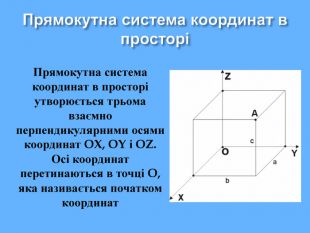
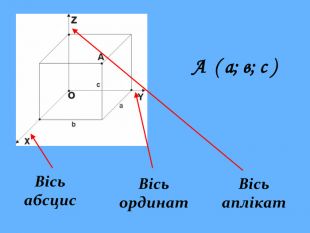
Урок "Координати у просторі"
Матеріал використаний для проведення позакласного заходу (тематичної консультації) для учнів 10 та 11 класів з метою систематизації та узагальнення знань учнів з теми «Координати у просторі», для учнів 10 класу - для підготовки до контрольної роботи; для учнів 11 класу – для підготовки до ЗНО з математики.
Серед матеріалів: розробка на 1 год, тематичні презентації.
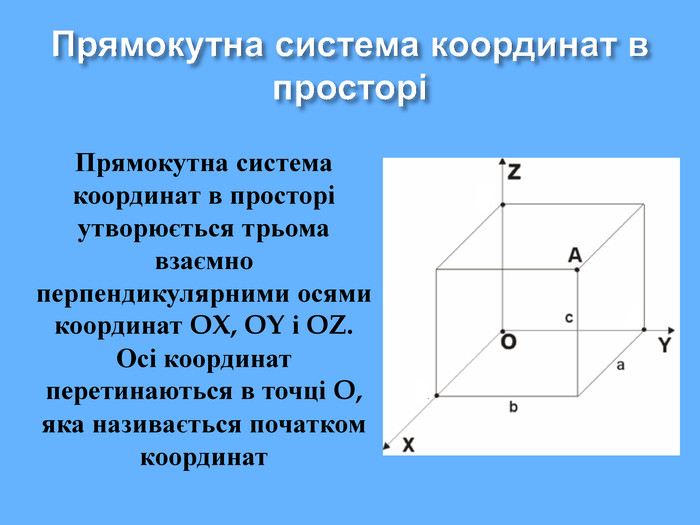
Координати у просторі
(консультація для учнів 10-11 класів, позакласний захід)
Мета:
- систематизація та узагальнення знань учнів з теми «Координати у просторі»,
- для учнів 10 класу - підготуватися до контрольної роботи;
- для учнів 11 класу – підготовка до ЗНО з математики;
- розширення кругозору учнів;
- розвиток інтересу до знань, логічного мислення
- виховання культури мовлення, уміння працювати в команді;
- формування активності, самостійності, кмітливості.
Обладнання: презентації учнів, роздавальний матеріал.
Форма заходу: гра команд. Вболівальники також виконують завдання (завдання виконане швидше команди і правильно приносить додатковий 1 бал на контрольній роботі з геометрії).
Тривалість заходу: 1 година.
Хід заняття
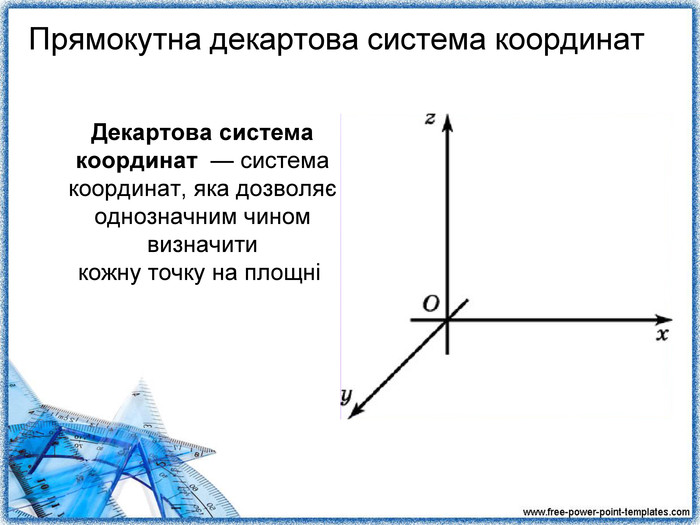
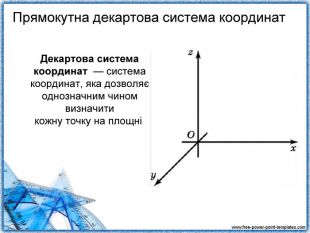
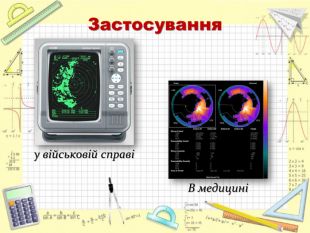
Вчитель: Розвиток систем координат в історії людства пов'язаний як з математичними задачами, так і з практичними проблемами мистецтва навігації, що спиралася на картографію та астрономію. Найвідомішу систему координат, прямокутну, запропонував Рене Декарт у 1637 році.
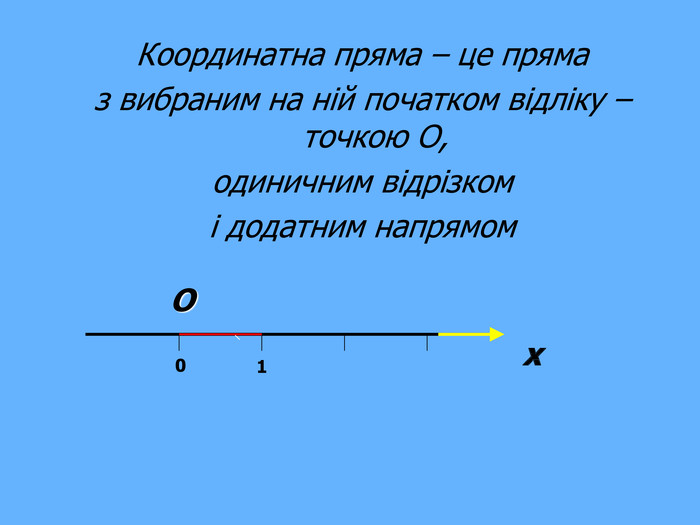
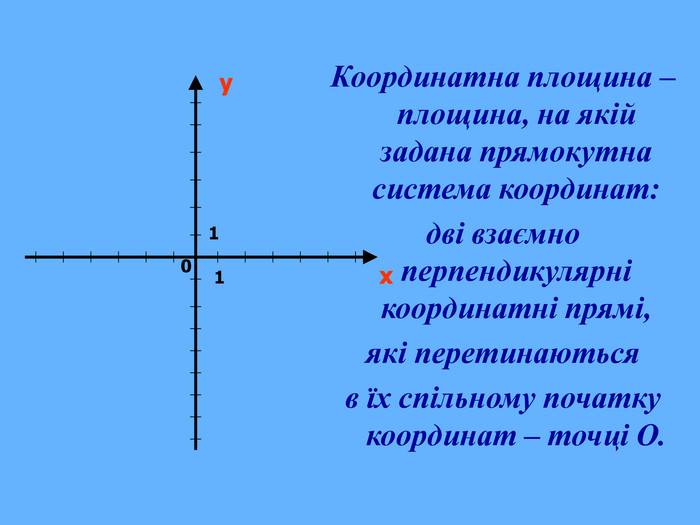
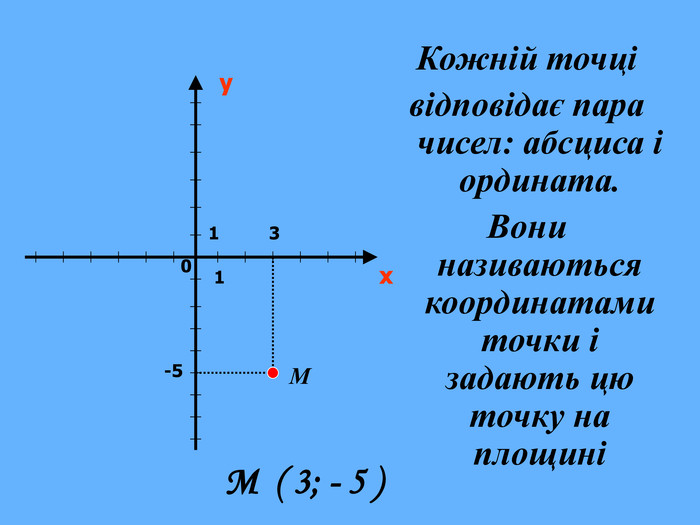
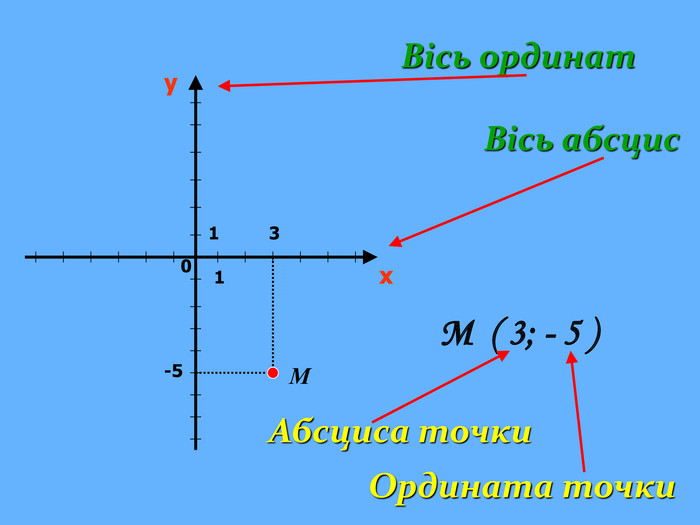
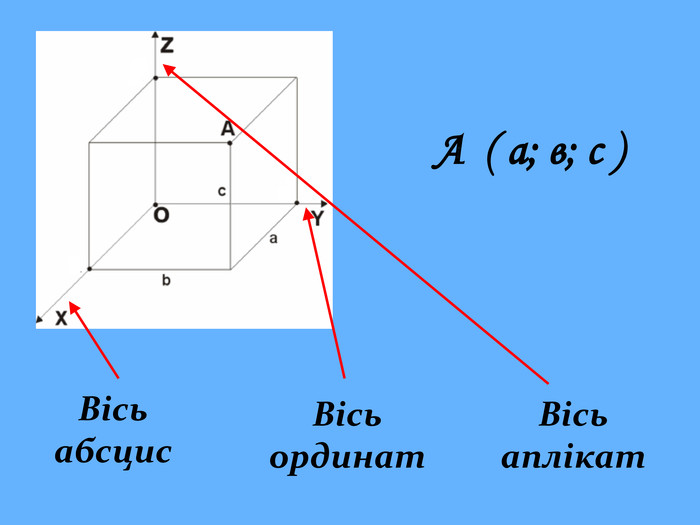
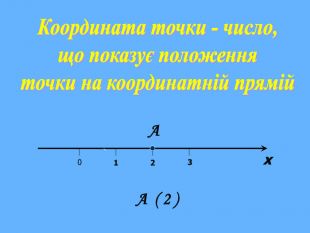
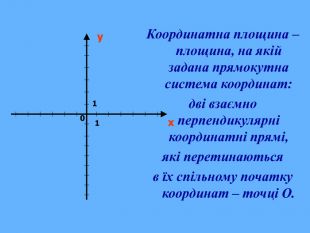
Що ж сьогодні відомо школярам про координати та їх системи? Давайте згадаємо (презентація 1 «Координати на прямій, площині, у просторі»)
Завдання 1. За наданими координатами поставити у декартовій системі координат у просторі точки. Команда, що виконає швидше, першою отримає підказку у вигляді загадки, розгадавши яку, отримає наступну підказку: назви відрізків для з’єднання точок.
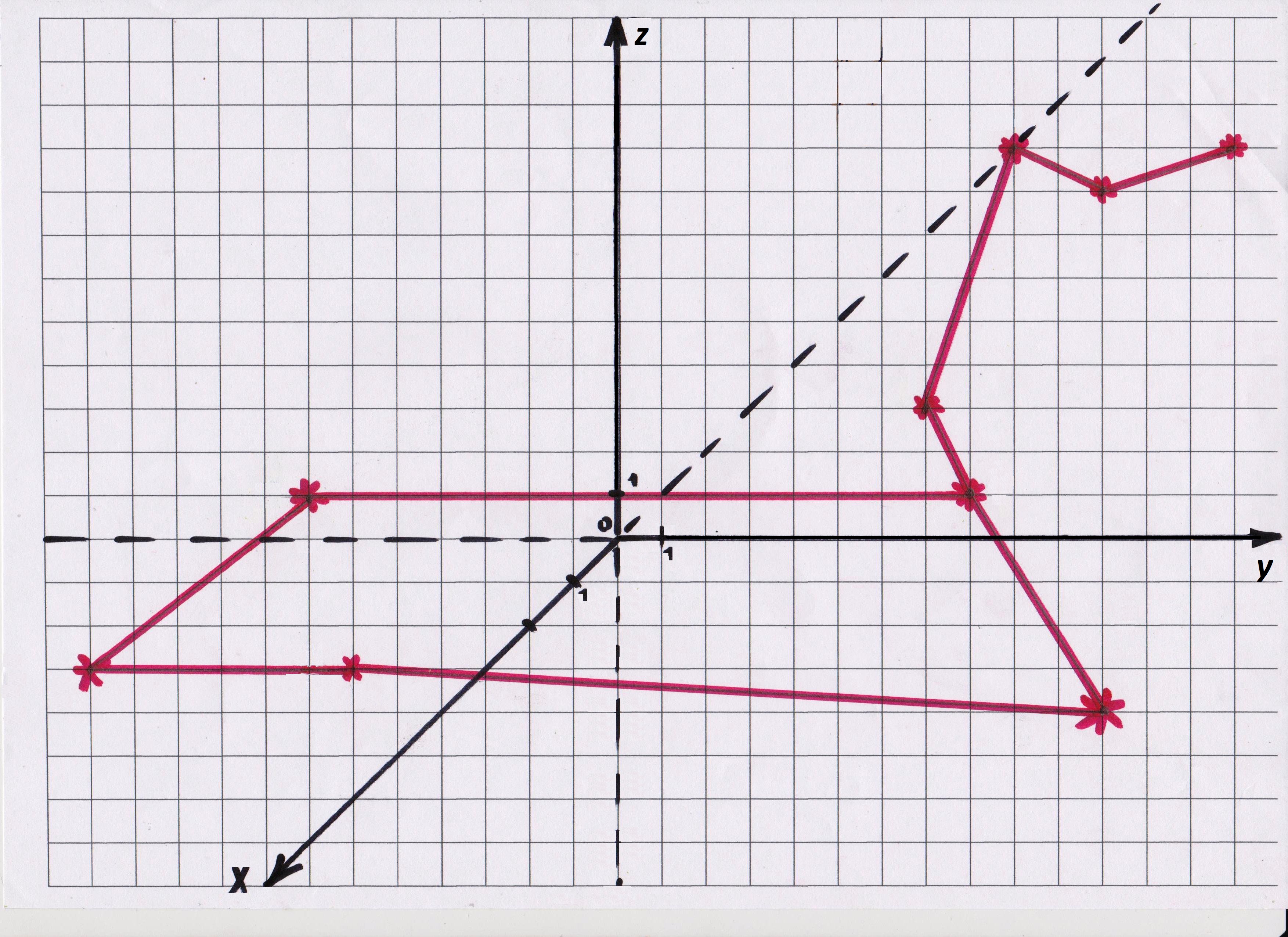
Точки: А(-1;-11;0), В(-5;-11;1), С(0;17;14), D(8;14;0), E(8;10;-2); F(0;0;-6); G(2;0;0), H(0;-4;-10); K(0;-4;0)
Підказка 1.
Гуде, як бджола,
Летить, як стріла,
Крила має,
Але не махає.
Підказка 2.
АВ, BC, CD, DE, EF, FG, GH, HK, AK, HF, KC, GC
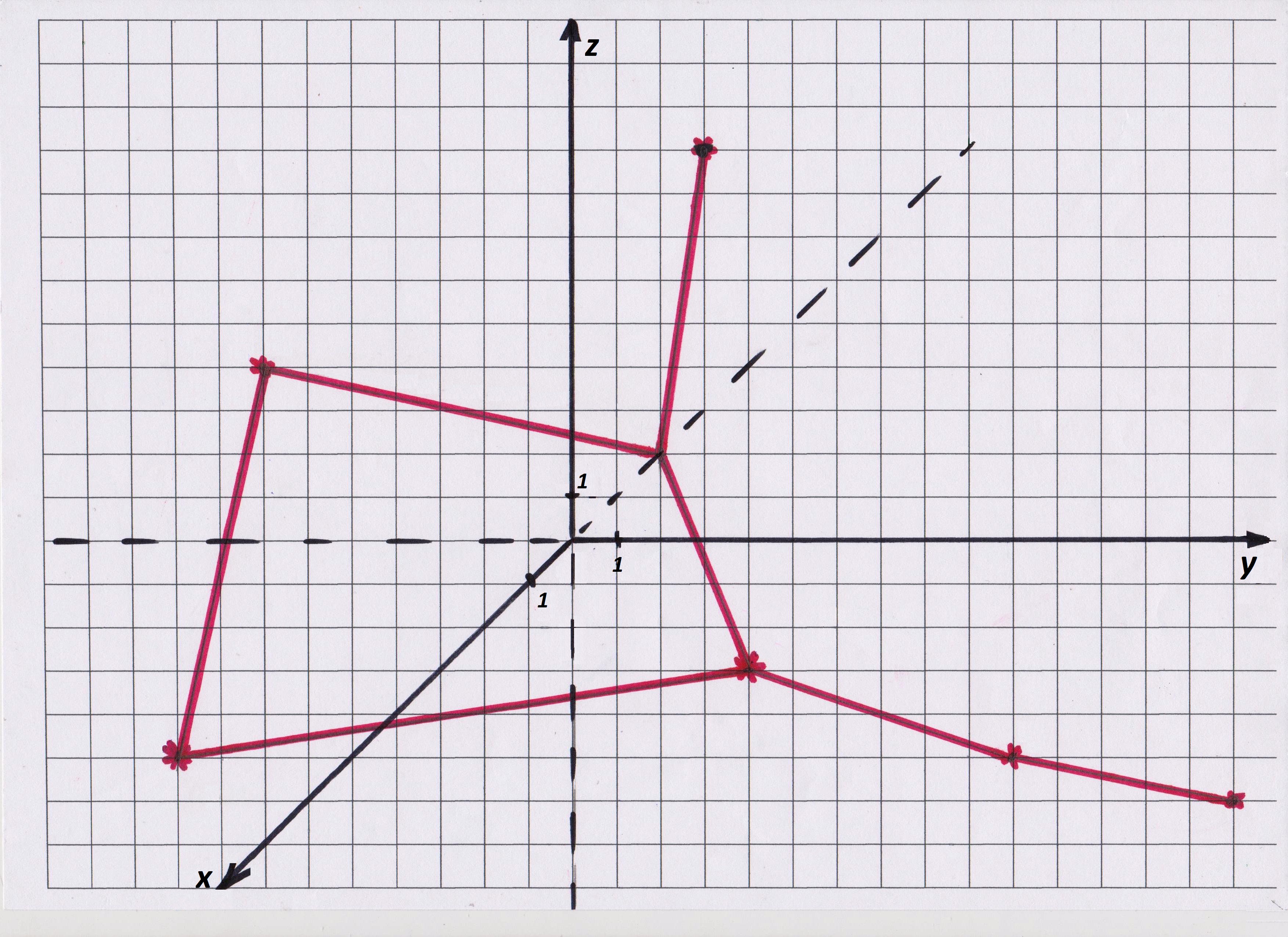
Результат роботи має бути таким (рис. 1):
Повідомлення учня 1: «З історії виникнення координат» (презентація 2).
Завдання 2. За наданими зображеннями визначити координати точок. Передати ці координати іншій команді, яка має за ними відтворити зображення.
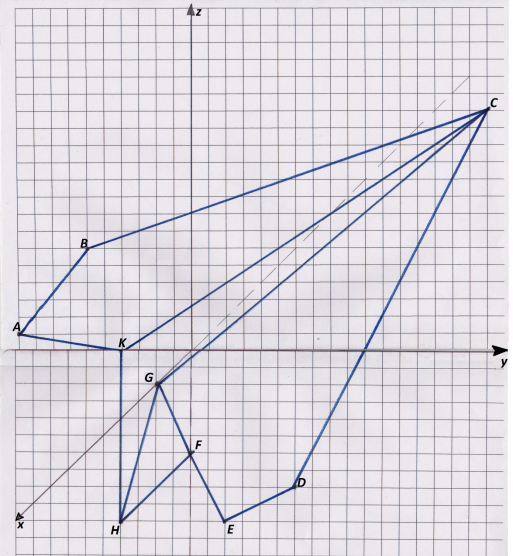
Зображення для команди 1.
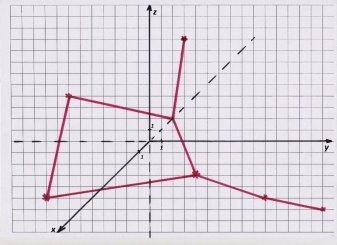
Зображення для команди 2.
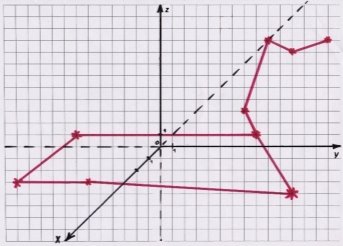
Цікава інформація. Отримані зображення – сузір’я Діви та Лева.
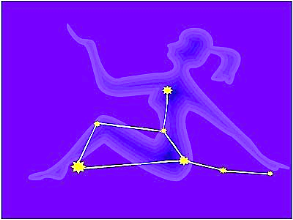
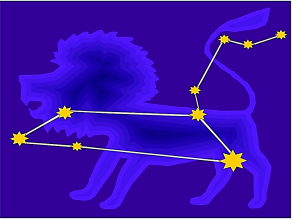
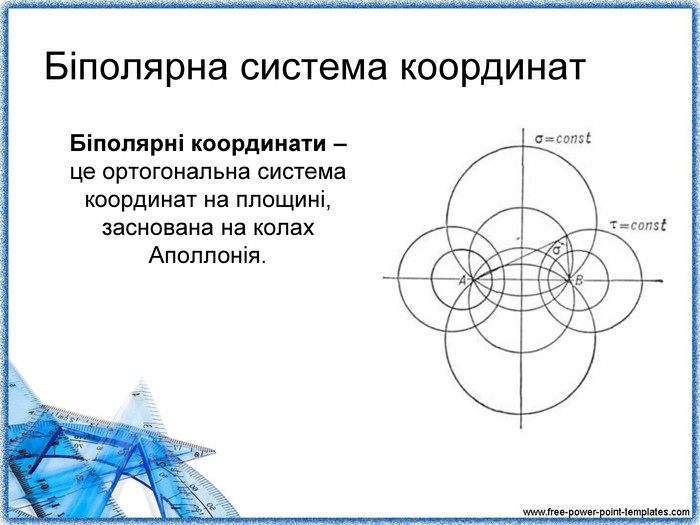
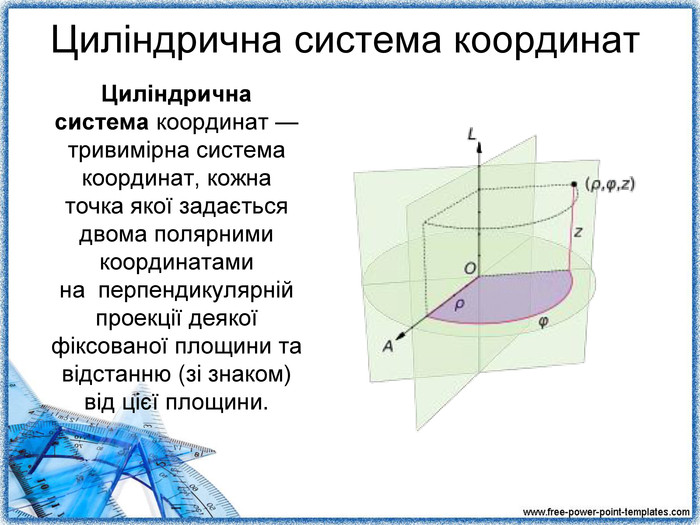
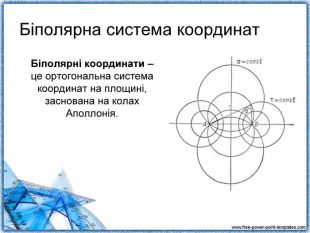
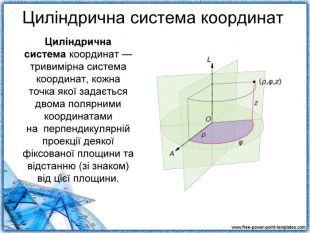
Повідомлення учня 2: «Різноманітність систем координат» (презентація 3).
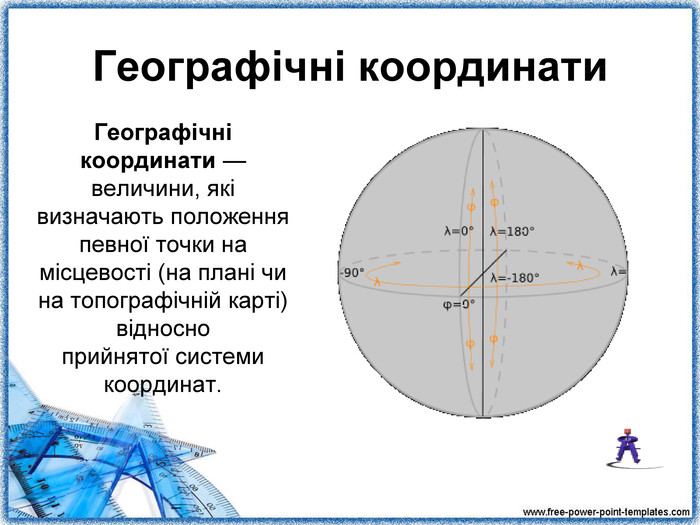
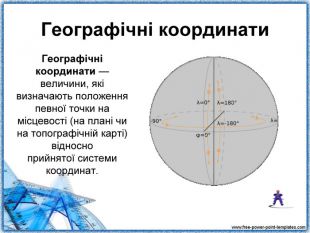
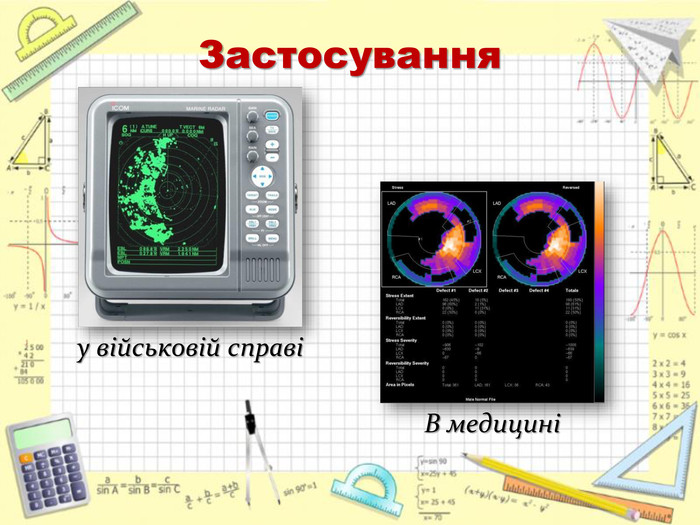
Виступ учителя географії «Географічні координати».
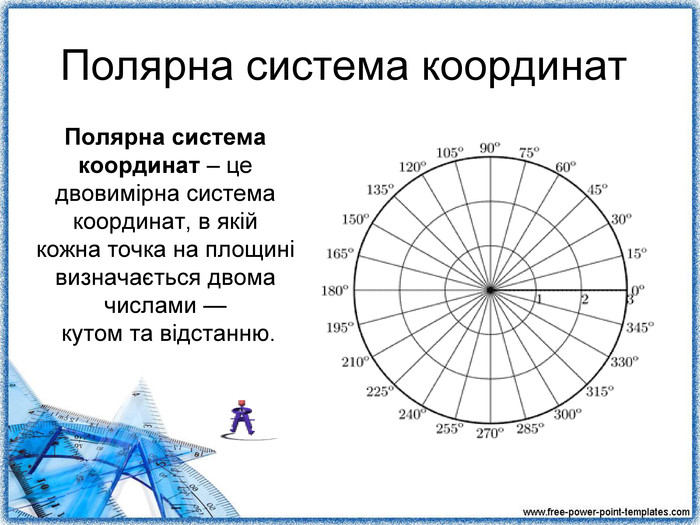
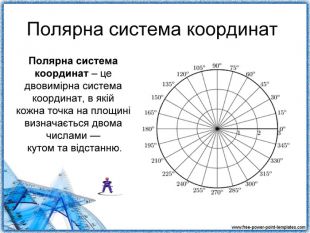
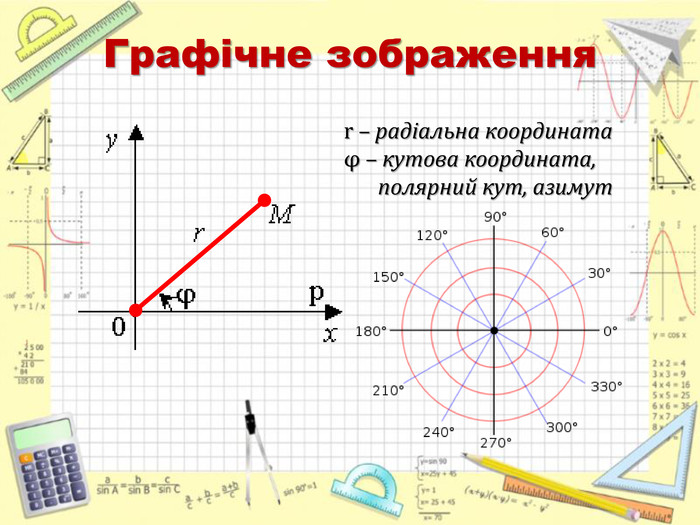
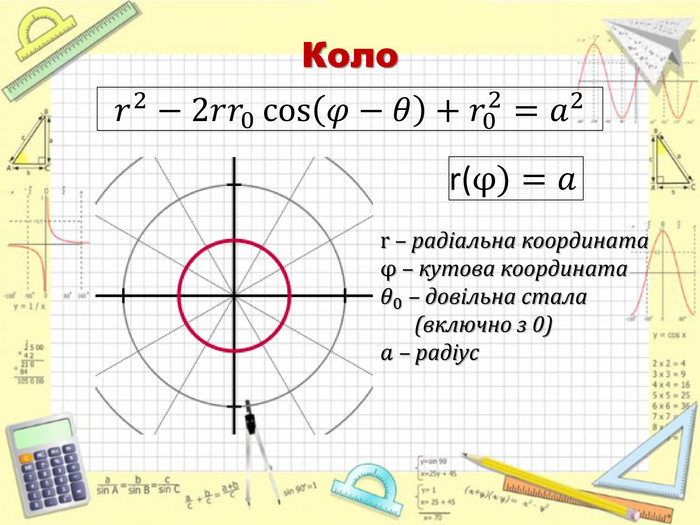
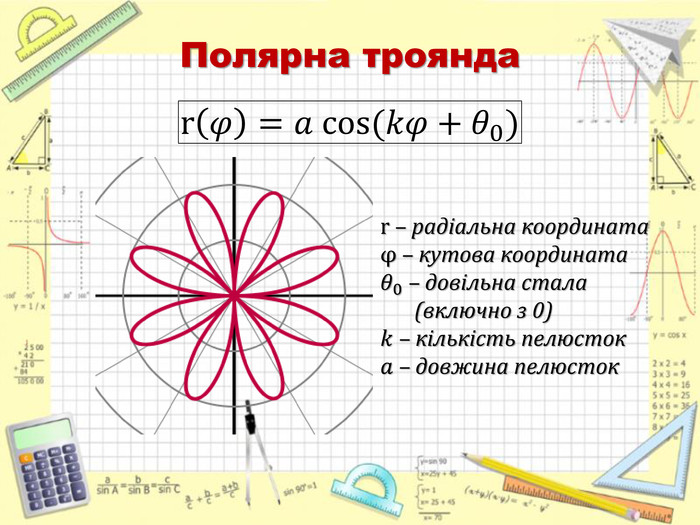
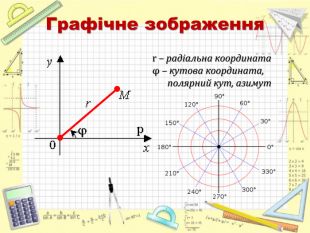
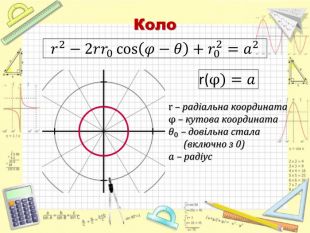
Повідомлення учня 3: «Полярна система координат» (презентація 4)
Завдання-підказки.
1. Історик ХХ століття Роуз сказав: «Це задушевна бесіда без слів, гарячкова активність, тріумф і трагедія, надія і відчай, життя і смерть, поезія і наука, Стародавній Схід і сучасна Європа»
2. Джерело багатьох математичних задач. Терміни з цієї області можна зустріти в літературі з програмування, кібернетиці.
3. Коли в кожній родині можна буде знайти цю гру, можна буде сподіватися на те, що з часом зникне убогість справжніх державних умів.
4. Батьківщина - Індія, вік - 15 століть. Ім'я винахідника невідомо. Давня старовинна назва - чатуранга.
5. Уродженець Праги на ім'я Стейніц першим прославив своє ім'я в зв'язку з цією грою.
6. Це постійна суперечка «двох К»
7. Це палацове життя в мініатюрі.
8. На квадратиках доски
Короли свели полки.
Нет для боя у полков
Ни патронов, ни штыков
Коментар учителя.
Відомий цікавий історичний факт: 16 грудня 1776 року відбулася велика битва при Трінстоне між британською армією на чолі з генералом Ролем і повсталими північноамериканських колоній. Генерал Роль забув прочитати донесення від своїх розвідників, так як був зайнятий грою. І битва була програна. Він грав в шахи.
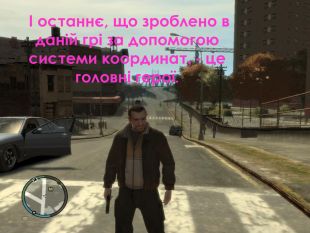
Повідомлення учня 4: «Координати в іграх» (презентація 5).
Завдання 3. Розв’язати тестові завдання та розшифрувати відповідь. Скласти ім’я відомого письменника.
Тестові завдання
- Знайдіть відстань між точками М(3;-4;1) та В(2;-1;0)
|
|
|
|
|
|
|
|
11 |
|
- Яка з наведених точок розташована на відстані 5 одиничних відрізків від початку координат?
|
|
|
|
|
|
А(1;1;3) |
В(-2;-1;-2) |
С(-3;0;4) |
D(5;5;5) |
- Знайдіть координати середини відрізка АВ, якщо А(8;3;-4), В(6;7;-2)
|
|
|
|
|
|
(7;5;-3) |
(1;-2;-1) |
(7;-2;-3) |
(-1;5;-1) |
- Точка К – середина відрізка MN, M(3;-1;4), K(2;5;-2). Знайти координати точки N.
|
|
|
|
|
|
(5;4;2) |
(2,5;2;1) |
(1;-6;6) |
(1;11;-8) |
- Укажіть точку симетричну точці А(2;-1;6) відносно початку координат
|
|
|
|
|
|
(2;1;6) |
(-2;-1;6) |
(-2;1;6) |
(-2;1;-6) |
- Укажіть точку, симетричну точці А(5;-2;3) відносно площини (ху)
|
|
|
|
|
|
(5;2;3) |
(5;-2;-3) |
(5;2;-3) |
(-5;2;3) |
- Паралельне перенесення задано формулами х1=х+1, у1=у-2, z1=z. У яку точку при цьому паралельному перенесенні переходить точка А(-2;3;4)?
|
|
|
|
|
|
(1;2;0) |
(2;-3;4) |
(-1;1;4) |
(1;-1;-4) |
- Яка з наведених фігур має тільки дві площини симетрії?
|
|
|
|
|
|
прямокутник |
трапеція |
півколо |
коло |
Шифр
Цікава інформація. Шифр «Танцюючі чоловічки» використаний в однойменному творі Артура Конан Дойля (1903 р.). Сам автор пізніше заніс цю історію до свого списку «12 улюблених історій про Шерлока Холмса».
Відповідь. Жуль Верн.
Питання до учнів. Як ви думаєте, чому ми згадали ім’я французького письменника Жуля Верна?
Очікувана відповідь. Жуль Верн був невтомним мандрівником. Багато його книг («П'ять тижнів на повітряній кулі», «Діти капітана Гранта», «20 000 льє під водою», «Навколо світу за вісімдесят днів», «П'ятнадцятирічний капітан» та багато інших) присвячені подорожам та відповідно змінам місцеположення головних героїв, що визначалися координатами.
Цікава інформація. Зі 108 наукових передбачень письменника-провидця на сьогодні не справдилося лише 10! (Вікіпедія)
Повідомлення учня 5: «Координати в літературі» (презентація 6).
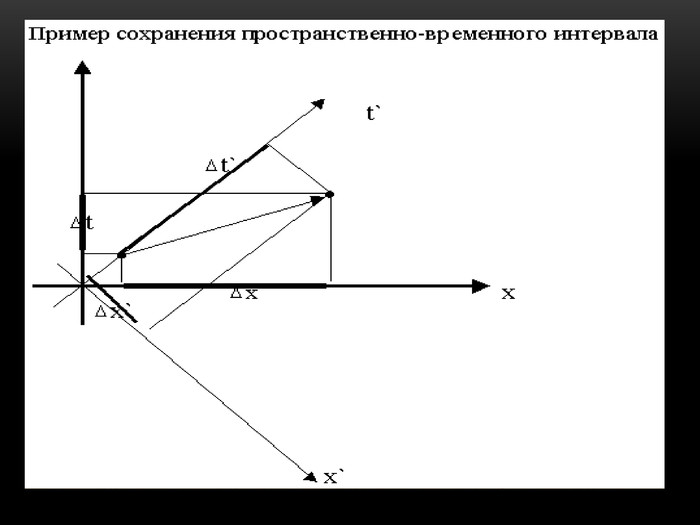
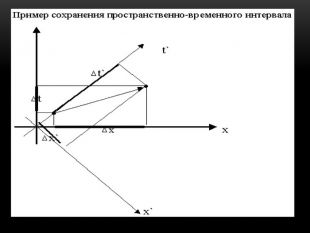
Повідомлення учня 6: «Простір Мінковського» (презентація 7).
Підведення підсумків заняття.
Використані джерела інформації.
- Колекція цифрових ресурсів Черкаського ОІППО [Електронний ресурс] – режим доступу oipopp.ed-sp.net
- Геометрія. 10 клас. Академічний рівень / О. О. Старова. –Х. : Вид.група «Основа», 2017. – (Серія «Мій конспект»)
- Жуль Верн [Електронний ресурс] – Режим доступу https://uk.wikipedia.org/wiki/%D0%96%D1%83%D0%BB%D1%8C_%D0%92%D0%B5%D1%80%D0%BD
- Танцюючі чоловічки [Електронний ресурс] – режим доступу https://uk.wikipedia.org/wiki/%D0%A2%D0%B0%D0%BD%D1%86%D1%8E%D1%8E%D1%87%D1%96_%D1%87%D0%BE%D0%BB%D0%BE%D0%B2%D1%96%D1%87%D0%BA%D0%B8
Координати точкина прямійта площині
01 ХКоординатна пряма – це прямаз вибраним на ній початком відліку – точкою О,одиничним відрізкомі додатним напрямом. О
0 А123 ХКоордината точки - число,що показує положенняточки на координатній прямій. А ( 2 )style.colorfillcolorfill.typefill.on
Координатна площина – площина, на якій задана прямокутна система координат:дві взаємно перпендикулярні координатні прямі,які перетинаютьсяв їх спільному початку координат – точці О.ху110
ху110 МКожній точцівідповідає пара чисел: абсциса і ордината. Вони називаються координатами точки і задають цю точку на площиніМ ( 3; - 5 )-53style.colorstyle.colorppt_x
ху110 ММ ( 3; - 5 )-53 Абсциса точки. Ордината точки. Вісь абсцис. Вісь ординат
Прямокутна система координат в просторі утворюється трьома взаємно перпендикулярними осями координат OX, OY і OZ. Осі координат перетинаються в точці O, яка називається початком координат
Вісьабсцис. Вісьординат. Вісьаплікат. А ( a; в; c )
1 У Декартовому морі є прямокутний острів на якому вчені посадили незвичайні пальми по кутах острова: Абрикосову, Виноградну, Сливову, Дубову. Кожна з них має свої координати: А (1; 1), В ( 1; 5), С (5; 5), D ( 5; 1). Знайдіть довжину берегів острова, та його площу. Одиничний відрізок – 1 км.0ху234512345 АВСDЗАДАЧА
Запитання. Що таке координатна пряма?Як утворюється система координат на площині?Як утворюється система координат в просторі?Яку назву має кожна координата точки в просторі?
З Колекції цифрових ресурсів на сайті Черкаського ОІППО
Історія виникнення координат. Підготувалаучениця 10 класу. Слободенюк Вікторія
Використання координатвизначення положення світил на небівизначення певних пунктів на Земліскладання зоряних і географічних карт
Згадки про перші координати Гіппарх. Оресм
Декартова площина. Рене Декарт
Приклади координат
Дякую за увагу!
Види систем координат
Полярна система координат. Полярна система координат – це двовимірна система координат, в якій кожна точка на площині визначається двома числами — кутом та відстанню.
Біполярна система координат. Біполярні координати – це ортогональна система координат на площині, заснована на колах Аполлонія.
Прямокутна декартова система координат. Декартова система координат — система координат, яка дозволяє однозначним чином визначити кожну точку на площні
Криволінійна система координат
Циліндрична система координат. Циліндрична система координат — тривимірна система координат, кожна точка якої задається двома полярними координатами на перпендикулярній проекції деякої фіксованої площини та відстанню (зі знаком) від цієї площини.
Сферичні координати. Сферичними координатами називають ситему координат для відображення геометричних властивостей фігури в трьох вимірах за допомогою задання трьох координат.
Географічні координати. Географічні координати — величини, які визначають положення певної точки на місцевості (на плані чи на топографічній карті) відносно прийнятої системи координат.
Дякую за увагу!
Полярна система координат. Підготувала учениця 10 класу. Степаненко Юлія
Історичні відомостіГіппарх. Архімед. Абу Райхан Біруні Алексі Клеро. Леонардо Ейлер
Графічне зображенняr – радіальна координатаφ – кутова координата, полярний кут, азимут
Зв'язок між декартовими та полярними координатами𝑥=𝑟cos𝜑 𝑦=𝑟sin𝜑 𝑟2=𝑦2+𝑥2 (По теоремі Піфагора)
Коло𝑟2−2𝑟𝑟0cos𝜑−𝜃+𝑟02=𝑎2 r – радіальна координатаφ – кутова координата𝜃0 – довільна стала (включно з 0)𝑎 – радіус r(φ)=𝑎
Полярна трояндаr𝜑=𝑎 cos(𝑘𝜑+𝜃0) r – радіальна координатаφ – кутова координата𝜃0 – довільна стала (включно з 0)𝑘 – кількість пелюсток𝑎 – довжина пелюсток
Архімедова спіральr𝜑=𝑎+𝑏𝜑) r – радіальна координатаφ – кутова координата𝑏 – відстань між витками
Застосуванняу військовій справіВ медицині
Дякую за увагу!!!
Системи координатв іграх
Система координатвикористовуєтьсяв простихкомп’ютерних іграх:шахах та морському бої
Ігрова дошка і є координатною площиною в шахах і шашках. А шашки або шахи є точками, які розміщені на цій координатній площиніppt_xxshearppt_xppt_xxshearppt_x
Текст надписи. Координати в тривимірному просторі формують трійку (x, y, z). Координати x, y, z для тривимірної системи координат можна розуміти як відстані від точки до відповідних площин: yz, xz, та xy. Тривимірна система координат є дуже популярною, тому що відповідає звичним уявленням про просторові виміри — висоту, ширину та довжину (тобто три виміри).
Це відома гра GTA 4. Ця гра виконана повністю тривимірною графікою.
Рельєф та рослини зроблені за допомого тривимірної графіки.
Система координат також використовується в засобах пересування.
І останнє, що зроблено в даній грі за допомогою системи координат, - це головні герої.
Запитання. Яким чином в іграх застосовується система координат?В грі “Морський бій” по-різному записують координати клітинок на ігровому полі. Які слова, літери використовуєте ви, коли граєте в цю гру?Назвіть ще відомі вам ігри, в яких використовується будь-яка система координат?
З Колекції цифрових ресурсів на сайті Черкаського ОІППО
Координати в. ЛІТЕРАТУРі
- ш и р о т а -довгота
Військові походи,морські пригодипов'язані зкоординатами
- ш и р о т а -довгота
- ш и р о т а -довгота. В багатьох пригодницькиххудожніх творах ми знаходимовикористання координат
Жюль Верн"Діти капітана Гранта"
Джек Лондон"Морські історії"
Роберт Л. Стівенсон"Острівскарбів"
… Наступні десять-дванадцять сторінок були заповнені якоюсь дивовижною бухгалтерією. З одного кінця рядка стояла дата, а з другого - сума. Але замість пояснювальних записів між датою і сумою стояло тільки різне число хрестиків. Щоправда, зрідка стояла ще назва місцевості, як-от: "Напроти Каракаса", або ж позначено було довготу й широту, як-от: “62°17'20н; 19°2'40т”. Біля останнього хрестика … червоним чорнилом дрібним чітким почерком було написано: "Більша частина скарбу тут".
Знаходження скарбу,певного місця чи предметана Землі неможливе без координат
Запитання. Пригадайте приклади використання координат в інших літературних творах. Чи використовували ви в своєму житті координати? Що це були за координати: відомі вже вам чи вами придумані? За яких обставин це відбувалося?
З Колекції цифрових ресурсів Черкаського ОІППО
Простір мінковського 1864 – 1909 рр.
Введено А. Пуанкаре і Г. Мінковським в 1907-08 рр. Простір Мінковського – чотиривимірний простір, що об'єднує фізичний тривимірний простір і час. Точки в просторі Мінковського відповідають подіям спеціальної теорії відносності. А. Пyанкаре першим встанов і детально вивчив одну з найважливіших властивостей перетворень Лоренца – їх групову структуру, і показав, що перетворення Лоренца є нічим іншим, як поворотом в просторі вимірів, точки якого мають координати (x,y,z,t) Положення події в просторі Мінковського задається чотирма координатами – трьома просторовими та однією часовою: x, y, z - прямокутні декартові координати події в деякій інерціальній системі відліку,координата ct, де t – час події, с – швидкість світла.
про публікацію авторської розробки
Додати розробку