Урок повторення вивченого матеріалу по темі "Радіанне вимірювання кутів"

Урок №  Дата______  Клас___11___  (алгебра)

Тема уроку: Повторення вивченого матеріалу: «Радіанне вимірювання кутів.

  Синус, косинус, тангенс кута

Мета уроку: повторити і узагальнити поняття радіанного вимірювання кутів; пояснити механізм    переведення кутів з радіанної міри в градусну та навпаки; формувати вміння переходити від однієї міри вимірювання кутів до іншої; сформувати означення синуса, косинуса, тангенса кута;

розвивати самостійне логічне мислення, вміння порівнювати, узагальнювати,  систематизувати, робити висновки, розвивати математичне мовлення;

виховувати світогляд учнів, культуру письма, почуття взаємоповаги.

Тип уроку:   узагальнення знань, умінь і навичок

Обладнання:  мультимедійний проектор, презентація, картки  з завданням для самостійної роботи, роздатковий матеріал для гри «Математичне доміно» підручник, повідомлення учнів

 

Хід уроку.

«Немає науки, не зв’язаної з математикою»

                          Л. Ейлер                (слайд 1)

І. Організаційний момент.

Привітання, організація роботи класу

 

ІІ. Перевірка домашнього завдання            (слайд 2)

1.Слово вчителя Тема, яку ми вивчали в рамках повторення і узагальнення вивченого матеріалу «Степенева функція».

Вчитель перевіряє наявність домашнього завдання в зошитах учнів, доки учні виконують завдання, поділившись на групи

2.Робота в групах (за завданнями на картках) 

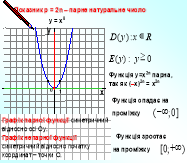
Завдання групі І. Намалювати схематично графік функції y = x² та дослідити її властивості

Завдання групі ІІ. Намалювати схематично графік функції y = x³ та дослідити її властивості

Завдання групі ІІІ. Намалювати схематично графік функції y =   та дослідити її властивості

3.Додаткові запитання як зміниться графік функції коли б вона мала такий вигляд: 1 група: а)у = x² +1; б)y = (x + 1)^2.

    2 група: а)у = x³ - 2; б)y = (x - 2)^3.

    2 група: а) y =  - 2 ; б) y =

                 

 

ІІІ. Мотивація навчальної діяльності.         (слайди 3-5)

  Слово вчителя.   Наприкінці ХV ст. італійський мандрівник Христофор Колумб відкрив узбережжя Америки. Португалець Васко да Гама відкрив морський шлях на Індію. Незабаром кораблі Магеллана вперше в історії зробили навколосвітню подорож. Почалася епоха великих географічних відкриттів, завоювань нових територій, освоєння незліченних багатств нових земель.

Не тільки окремі групи купців і мореплавців, але і цілі держави боролися за право експлуатації нових земель. Потрібні були більш потужні і швидкохідні судна, точні географічні карти, досконалі способи орієнтування в відкритому океані.

Все це і багато чого іншого привело до необхідності розвивати астрономію – науку про рух небесних тіл, та він був неможливий без розвитку тригонометрії.

  Тому в шкільному курсі обов’язковою є тема «тригонометричні функції та їх властивості, графіки», яку ми вивчаємо в рамках повторення і узагальнення вивченого матеріалу.

 

ІV. Актуалізація опорних знань .

1. Слово вчителя.   Тригонометричні функції, означені у курсі математики як функції кута. Водночас різні задачі з математики, фізики, економіки та інших наук приводять до тригонометричних функцій, аргументами, яких є не кути, а інші величини (довжина, час, температура тощо). Тому в математиці тригонометричні функції розглядають як функції числового аргументу, які в першу чергу використовують для опису різноманітних періодичних процесів.

2. Фронтальне опитування

Щоб перейти до їх вивчення теми пригадаємо:

З тригонометричними функціями ви працювали коли, вивчали трикутники, а саме прямокутний трикутник.

Спробуйте для елементів прямокутного трикутника встановити відповідність:

       (слайд 6 )

 

 

                       c

а

 

 

 

                        b

 

А)   sin                        А) відношення протилежного катета до прилеглого

Б)   cos                         Б) відношення протилежного катета до гіпотенузи

В)   tg                         В) відношення прилеглого катета до протилежного

Г)   ctg                        Г) відношення гіпотенузи до прилеглого катета

                                      Д)  відношення прилеглого катета до гіпотенузи

• Що таке коло?(Геометрична фігура, яка складається з усіх точок площини,      розміщених на даній відстані від даної точки – центра кола)                      (слайд 7)

3. Метод аналогій                      (слайд 8)

• Що таке радіус (Радіус – це відрізок, що сполучає центр кола з якою-небудь його точкою)                                                                                                                                      (слайд 9)
•              Що таке кут? (Два промені, що виходять з однієї точки)                 (слайд 10)
•              Які ви знаєте кути?(Гострий, тупий, прямий, розгорнутий)
•              Який кут називається центральним? (Кут з вершиною в центрі кола)
•              Які вам відомі одиниці вимірювання кутів? (Градус)        (слайд 11)
•              Число π               (слайд 12)

4.Історична довідка              

5.Слово вчителя Наше завдання навчитися замінювати градусну міру кута на число. У математиці, фізиці використовують іншу одиницю вимірювання кутів , тому що до градусної міри не  можна додати число.

 Цю одиницю вимірювання називають радіаном.

6.Повідомлення теми і мети уроку

 Отже, тема нашого уроку: «Радіанне вимірювання кутів. Синус, косинус, тангенс кута».                                                                                                    (слайд 13)

 

V. Формування нових знань.

Розповідь вчителя. Ми з вами сьогодні з’ясуємо що таке радіан.      (слайд 14)

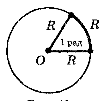Радіан — це центральний кут, який опирається на дугу, довжина якої дорівнює радіусу (рис.1).                                                                                          (слайд 15)

 

 

 

 

 

Установимо зв’язок між радіанним і градусним вимірюванням кутів. В зв’язку з тим, що радіанна міра кута в 180° дорівнює π:   180° = π рад.

 Розділивши ліву і праву частини рівності на 180, одержуємо

1° = рад, або 1° 0,017 рад.

Розділивши ліву і праву частини рівності на π ,одержуємо

1 рад = , або 1 рад 57°.

Розглянемо приклади переходу від радіанної міри до градус­ної і навпаки.  (слайд 16)

Приклад 1. Визначить в радіанах величини кута 30°

Складаємо пропорцію:

180⁰   -   π
30⁰     -   х

Х= 30π/180

Відповідь:

          α = 30⁰ =

Приклад 2. Визначить в градусах величини кута         (слайд 17)

Дано: кут α =      .
Треба: перевести в градуси.

Пам’ятаємо, що π = 180⁰

 

          α  ===

При записі радіанної міри кута позначення «рад» опускають. Наприклад, замість рівності 90° = рад, пишуть 90° = .

 

VI. Формування вмінь і навичок

1.  Розв'язування вправ.

Розглянемо приклади переходу від радіанної міри до градус­ної і навпаки.

1. Запишіть у радіанній мірі кути 30°;  45°;  60°;  90°  180°.

2. Визначить у градусах кут, радіанна міра якого дорівнює даному числу

;;;

 

2. Розповідь вчителя « Системи вимірювання кутів в житті людини»

В астрономії, техніці, морській справі та в інших галузях використовують інші одиниці вимірювання кутів.                                                                                                                   (слайди 18-23)

 

3. Приклад розв'язування компетентісної задачі                  (слайд 24)

Який кут пройде велика стрілка годинника, якщо годинник показуватиме 12 годин 40 хвилин?                                         

4. Гра «Математичне доміно» Робота в групах        (слайд 25)

Фрагмент гри в доміно імпровізованими картками з позначеннями кутів у градусній і радіанній мірі. За певний час група повинна скласти «рибу», чи послідовність карток.

            

VIІ. Формування нових знань.

Розповідь вчителя. Розглянемо  одиничне коло з радіусом 1                                      (слайд 26)

В точці М. може бути багато різних точок           (слайд 27)

Розглянемо коло  r =1          (слайд 30-31)

Основні тригонометричні тотожності : синусом кута називається ордината у, а косинусом кута – абсциса х.                           

Знаки тригонометричних функцій                     (слайд 32)

 

 

 

 

Таблиця значення деяких тригонометричних кутів                 (слайд 33)

α	0					π		2π
	0°	30°	45°	60°	90°	180°	270°	360°
sin α	0				1	0	-1	0
cos α	1				0	-1	0	1
tg α	0		1		не існ.	0	не існ.	0
ctg α	не існ.		1		0	не існ.	0	не існ.

 

 

VІІІ. Формування вмінь    

 Виконання  вправ    «Коло ідей»

1. Синус якого числа на вiдрiзку дорiвнює:  а) 0; б) 1; в) ; г) ?

2. Косинус якого кута вiдрiзка дорiвнює:  а) 0; б) 1; в) ; г) ?

3. Укажiть декiлька значень , при яких: а) ; б) ; в) ; г) ; д) ; е) не існує.

 

IX. Домашнє завдання.

1. Повторити «»Тригонометричні функції числового аргументу.  
2. Виконати задачу:  “Який кут пройде велика стрілка, якщо годинник показуватиме 12 годин, 50 хвилин”     (слайди 34-35)
3. Заповнити таблицю користуючись одержаними на уроці формулами.

Градуси	30º	45º		90º		135º		180º		360º
Радіани			π/3		2π/3		5π/6		3π/2

 

X. Підсумок уроку.

1.Рефлексія              (слайд 35)

Доповніть речення:

Сьогодні я навчився…

Мені було не зрозуміло….

Я хотів би дізнатися…

2.Оголошення оцінок за роботу учнів на уроці          (слайд 36)

3.Підсумкове слово вчителя.

Сьогоднішній урок я хотів би закінчити словами Сократа:    (слайд 36)

«Те, що я встиг пізнати, ­– чудове. Сподіваюся, таке ж чудове те, що мені ще доведеться пізнати»                                                                                            

 

Дякую за увагу!               (слайд 37)

Додаток 1

Картка для роботи учня на уроці (Група 1)

1. Робота в групах (за завданнями на картках) 

Завдання групі І. Намалювати схематично графік функції y = x² та дослідити її властивості

Додаткові запитання як зміниться графік функції коли б вона мала такий вигляд: а)у = x² +1; б)y = (x + 1)^2.

 

 

Картка для роботи учня на уроці (Група 2)

1. Робота в групах (за завданнями на картках)

Завдання групі ІІ. Намалювати схематично графік функції y = x³ та дослідити її властивості

 

Додаткові запитання як зміниться графік функції коли б вона мала такий вигляд:     а)у = x³ - 2; б)y = (x - 2)^3.

 

Картка для роботи учня на уроці (Група 3)

1. Робота в групах (за завданнями на картках)

Завдання групі ІІІ. Намалювати схематично графік функції y =   та дослідити її властивості

Додаткові запитання як зміниться графік функції коли б вона мала такий вигляд:     а) y =  - 2 ; б) y =