Урок, "Прямокутний трикутник"

Клас: 7-А

Дата: 20.02.2013

Вчитель: Пусан В.В.

Тема. Прямокутний трикутник. Розв’язування задач

Мета: домогтися засвоєння учнями властивості прямокутного трикутника з гострим кутом 30° та оберненого твердження і схеми їх доведень; сформувати в учнів уміння відтворювати формулювання цих тверджень та використовувати їх для розв’язування задач; удосконалювати вміння використовувати набуті раніше знання для розв’язування задач на прямокутний трикутник.

Тип уроку: засвоєння знань, умінь та навичок.

План уроку

I. Організаційний момент (2 хв.)

II. Перевірка домашнього завдання(7 хв.)

III. Розв’язування задач (25 хв.)

IV. Підсумки уроку (8 хв.)

V. Домашнє завдання (3 хв.)

ХІД УРОКУ

I. Організаційний момент

II. Перевірка домашнього завдання

Математичний диктант

1. Закінчіть речення: «Трикутник, у якого є прямий кут, називається...»

2. У прямокутному трикутнику один з кутів дорівнює 47°. Чому дорівнюють два інші його кути?

3. Закінчіть речення: «Сторона прямокутного трикутника, що лежить проти прямого кута, називається...»

4. Гіпотенузи двох прямокутних трикутників рівні. Один з кутів першого трикутника дорівнює 40° та один з кутів другого дорівнює 50°. Чи рівні ці трикутники? Чому?

5. У трикутнику ABC кут А прямий. Чим є в цьому трикутнику сторона AB?

6. У прямокутних трикутниках ABC і XTY рівні катети BC і TY та гіпотенузи AB і XT. Що можна сказати про ці трикутники? Чому?

III. Розв’язування задач

Завдання. Визначте довжину відрізків, позначених буквою x на рисунку 1 у кожному випадку, якщо всі зображені трикутники рівносторонні.

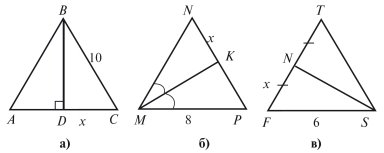
Порівняйте знайдені величини з довжиною сторони даного трикутника. Зробіть загальний висновок.

Виконання усних вправ

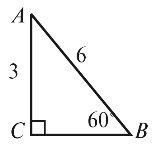
1. На рисунку 3 за даними, вказаними на рисунку, знайдіть невідомий елемент x.

2. Гіпотенуза прямокутного трикутника 10 см, один з гострих кутів цього трикутника вдвічі більший за інший. Знайдіть катет, що лежить при більшому гострому куті трикутника.

Виконання письмових вправ

Задача. У прямокутному трикутнику один з гострих кутів дорівнює 60°, а сума гіпотенузи та меншого катета дорівнює 18 см. Знайти гіпотенузу.

Дано:   ΔАВС;    С =90°                                                      А

АВ + ВС=18 см;

  В = 60°

Знайти: АВ.                                                                         

Розв’язання:                                                              В                        С                                 

А =90° - 60° = 30°,

тому що Δ АВС — прямокутний,   тоді АВ = 2 ВС.

Нехай: ВС = х см;   АВ = 2х см,    тоді за умовою задачі  2х + х = 18 см . Отже   АВ = 12 см.

Відповідь: АВ = 12 см.

1. Один із кутів прямокутного трикутника дорівнює 60°, а різниця між гіпотенузою і катетом, прилеглим до даного кута, становить 6 см. Знайдіть ці сторони трикутника.

2. У прямокутному трикутнику катет, прилеглий до кута 30°, дорівнює 18 см. Знайдіть довжину бісектриси трикутника, проведеної до даного катета.

3. У прямокутному трикутнику катет довжиною 12 см, прилеглий до кута, що дорівнює 30°. Знайдіть довжину бісектриси іншого гострого кута трикутника.

На закріплення матеріалу попереднього уроку можна розв’язати такі задачі:

1. У трикутнику ABC висота AD ділить кут A на два кути, причому Знайдіть кути трикутника ABC.

2. Висота рівнобедреного трикутника, проведена до бічної сторони, утворює з основою трикутника кут 35°. Знайдіть кути даного трикутника.

3. Доведіть рівність прямокутних трикутників за катетом і висотою, проведеною до гіпотенузи.

IV. Підсумки уроку

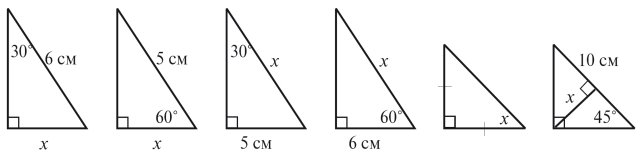
Чи існує прямокутний трикутник, зображений на рисунку 4? Чому?

V. Домашнє завдання

Вивчити теоретичний матеріал.

Письмово розв’язати задачі.

1. Доведіть рівність прямокутних трикутників за катетом і бісектрисою, проведеною до гіпотенузи.

2. У рівнобедреному трикутнику ABC з основою AC висоти AD і BE перетинаються під кутом 50°. Знайдіть кути даного трикутника.