Урок з алгебри для 11 класу на тему: « Показникові рівняння з параметрами»

Конспект уроку з алгебри для 11 класу на тему:

 « Показникові  рівняння з параметрами»

Формування компетентностей:

• предметна(математична) компетентність: сформувати вміння розв’язувати нескладні показникові  рівняння з параметрами;
• ключові компетентності:
• спілкування державною мовою – уміння ставити запитання й розпізнавати проблему; грамотно висловлюватися рідною мовою; доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку;
• уміння вчитися впродовж життя – уміння визначати мету навчальної діяльності, відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети;
• основні компетентності у природничих науках і технологіях – усвідомлення важливості математики як універсальної мови науки, техніки та технологій;
• соціальна та громадянська компетентності – уміння аргументувати та відстоювати свою позицію; співпрацювати в команді.

Тип уроку: засвоєння нових знань і вмінь.

Хід уроку

1. Організаційний етап.
2.  Перевірка домашнього завдання (заданого за підручником).
3. Актуалізація опорних знань.

1.     Бесіда.

Термін «параметр» - це термін грецького походження, у перекладі означає «відміряти». Поняття параметра є у різних науках, наприклад, фізиці, хімії, програмуванні, економіці та ін. Під поняттям параметра розуміють величину, якою характеризують певну властивість, стан, розмір або форму об’єкта, робочого тіла, явища, системи та інше. До необхідності розв’язувати завдання з параметрами( в межах побудованої математичної моделі ) приводить велика  кількість математичних задач, зокрема, економічних, технічних, медичних.

Можна сформулювати таке означення завдання з параметром.

Рівняння з параметром – це таке рівняння, до запису якого крім змінної та числових коефіцієнтів входять буквенні коефіцієнти, які є величинами, значення яких не вказані конкретно, але вони вважаються відомими та заданими на деякій числовій множині. Наприклад, 2х – а=0 із змінною х  та параметром а.

Розв’язати рівняння з параметром – це означає для кожного значення параметра а встановити, чи має рівняння розв’язки; якщо так, то знайти ці розв’язки, які, як правило, залежать від параметра а.

2.     Виконання усних вправ.

Розв’яжіть залежно від значень параметра а рівняння:

а)2х = а; б) ах = 8; в) х² = а + 2.

3.     Фронтальне опитування.

1. Сформулювати означення та властивості степеня з довільним дійсним показником.
2. Зобразити графік показникової функції та назвати її властивості.

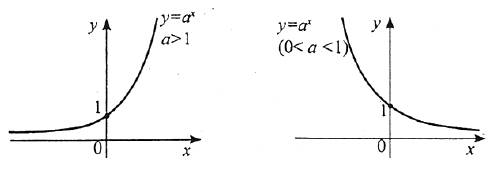
3. Сформулювати наслідок із властивості монотонності показникової функції (якщо степені того самого числа, відмінного від одиниці, рівні, то рівні й їх показники).

4. Вивчення нового матеріалу.

План вивчення теми

1.     Рівняння зі змінною х та параметром а будемо називати показниковим, якщо змінна входить до показника степеня.  Наприклад:1)  2^х = а; 2) 3^ах =3^2х-1.

 

2)Приклади розв’язання показникових рівнянь із параметрами.

Приклад 1. Розв’яжіть рівняння з параметром а^х = b.

Розв’язання. Дане рівняння показникове.

1)  має один корінь, якщо b>0;

2)   не має коренів, якщо b≤0.

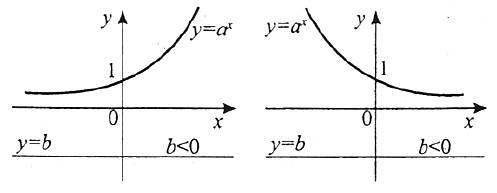
Приклад 2.  Розв’яжіть рівняння з параметром а:

Розв’язання. 1. Дане рівняння – показникове. І змінна х, і параметр а можуть приймати будь-які дійсні значення.

 2. Введемо заміну: 2^х = t, де t0. Отримаємо квадратне рівняння відносно нової змінної t . Розв’яжемо утворене рівняння.

t² – (2a + 1)t + (a² + a) =0,

А = 1, В = – (2a + 1), С = a² + a,

D = a² + a) = 4а² + 4а + 1 – 4а² – 4а = 1, отже, квадратне рівняння при будь-яких значеннях параметра буде мати два різні корені:

t₁ = ,   t₂ = .

3.Повернемося до заміни.

3.1 Коли з t₁ можна повернутися до заміни?

Тоді, коли t₁ , тобто t₁ = а ; отже, якщо а є (0; +∞), то повертаємось до заміни 2^х = а,  =   х =

3.2 Коли з t₂ можна повернутися до заміни?

Тоді, коли t₂ , тобто t₂ = а + 1 для а ; отже, якщо а є (-1; +∞), то повертаємось до заміни 2^х = а + 1,   х =

4.Позначимо знайдені розв’язки на прямій параметра та запишемо відповідь

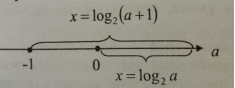
  Відповідь. 1) Якщо а є (-∞ ; -1], то х є ∅ ;

2.                 якщо а є (-1; 0), то х =
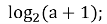
3.                 якщо а = 0, то х = 0;
4.                 якщо а є (0; +∞), то   х = 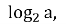х =

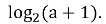
5.               Засвоєння нових знань і способів дій.

1.               Робота з підручником.

Розв’язування вправи 2.24

При яких значеннях параметра а рівняння 9^х – (а + 1)3^х + 3а – 6 = 0 має єдиний корінь?

Розв’язання. 1. Дане рівняння – показникове. І змінна х, і параметр а  можуть приймати будь-які дійсні значення.

2. Введемо заміну: 3^х = t, де t0. Отримаємо квадратне рівняння відносно нової змінної t . Розв’яжемо утворене рівняння.

t² – (a + 1)t + (3а - 6) =0,

А = 1, В = – (a + 1), С = 3а - 6,

D = ) = а² + 2а + 1 – 12а +24 = а² -10а + 25 = , отже квадратне рівняння при будь-яких значення параметра буде мати два різні корені:

t₁ = ,   t₂ = .

3.Повернемося до заміни.

3.1 Коли з t₁ можна повернутися до заміни?

Тоді, коли t₁ , тобто t₁ = 3 ; отже, 3^х = 3, х = 1

3.2 Коли з t₂ можна повернутися до заміни?

Тоді, коли t₂ , тобто t₂ = а - 2 для а .

Для виконання умови задачі рівняння 3^х = а – 2 не повинне мати коренів або мати єдиний корінь х = 1. Якщо а ≤ 2, то а – 2 ≤ 0 і рівняння 3^х = а – 2 не має коренів. Число 1 є коренем цього рівняння, якщо 3^х = а – 2, а = 5.

  Відповідь. а є (-∞ ; 2] або а = 5.

6. Удосконалення знань і вмінь.

Робота в парах.

Обговоріть план виконання завдань. Виконайте завдання. Здайте роботу вчителеві на перевірку.

Варіант 1

Розв’яжіть рівняння з параметром а:

Вказівка. Введіть заміну 5^х = t, де t0.

Відповідь . 1) Якщо а є (-∞ ; -1), то х₁=  х₂=;

2.     якщо а = -1, то х = 0;
3.     якщо а = 0, то х є ∅; 
4.     якщо а є (0; +∞), то   х =

 

 

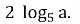
Варіант 2

Розв’яжіть рівняння з параметром а:

          Вказівка. Введіть заміну 2^х = t, де t0.

Відповідь. 1) Якщо а є (-∞ ; 0), то х =  ;

2.     якщо а = 0, то х є ∅; 
3.     а є (0 ; 1)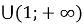, то х₁ =  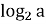; х₂ = 2 ;
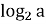4.     якщо а = 1, то х = 0.

7. Підбиття підсумків уроку, рефлексія.

Підсумкова бесіда.

• Що ми сьогодні робили на уроці?
• Як ми це робили?
• Чи досягли мети уроку?
• Для чого нам потрібні ці знання?
• Як працювалося в парах?

 

8. Домашнє завдання.

Завдання за підручником: п.2, вправа  2.26.

Розв’яжіть рівняння з параметром а (завдання НМТ 24):

1. Знайдіть суму всіх цілих значень параметра а, за яких усі корені рівняння

4^х - 152^х – 4а² +30а = 0 є додатніми.

2. Знайдіть найбільше значення параметра а, за якого не має коренів рівняння

3^х + (4а² +10а) 3^-х =4а + 5.

Література

1. Мерзляк А.Г.  Алгебра і початки аналізу: проф. рівень: підруч.  для 11 кл. закладів загальної освіти/ А.Г Мерзляк, Д.А. Номіровський, В.Б. Полонський та ін. – Х.: Гімназія, 2019.
2. Прус А.В., Швець В.О. Задачі з параметрами в шкільному курсі математики. Видання друге, доповнене. Навчально-методичний посібник. – Житомир: Видавництво ПП «Рута», 2018, 544с.
3. Карпік В.В. Алгебра та початки аналізу. 11 клас. Профільний рівень. I семестр / В.В. Карпік. – Х. : Вид. група «Основа». 2020. – 204, - (Серія

« Мій конспект»).

4. Репета Віктор, Клешня Надія, Коробова Марина, Репета Леся. Задачі з параметрами. Розв’язки з параметрами. Розв’язки, рекомендації, приклади: Навчальний посібник для старшокласників та абітурієнтів. – Тернопіль: Підручники і посібники, 2002. – 264с.