Урок з алгебри в 11 класі на тему:"Побудова графіка функції за допомогою похідної"
Допомогти учням «відкрити» способи побудови графіка функції за допомогою похідної. Скласти загальну схему дослідження і побудови графіка функції. Розвивати логічне мислення, уміння аналізувати, порівнювати, бачити аналогію задач.
Формувати єдину наукову картину світу.
Урок2.Тема: Побудова графіка функції за допомогою похідної.
Вчитель КЗШ№45-Ласкіна С.М
Тип: Урок засвоєння нових знань.
Мета: Допомогти учням «відкрити» способи побудови графіка функції за допомогою похідної. Скласти загальну схему дослідження і побудови графіка функції. Розвивати логічне мислення, уміння аналізувати, порівнювати, бачити аналогію задач.
Формувати єдину наукову картину світу.
Хід уроку.
Ι- Організаційний момент.
ΙΙ- Пояснення нового матеріалу.
Проблема: Як побудувати графік функції у=3х![]() -4х
-4х![]() .
.
Давайте припустимо що графік деякої функції побудовано. Наприклад:
|
Питання вчителя |
Очікувана відповідь. |
|
- Які властивості функції визначають поведінку графіка функції?
-як знайти проміжки зростання, спадання функції? |
Треба дослідити функцію на монотонність. Якщо f '(x)>0 на проміжку (а;в), то функція зростає на (а;в). Якщо f '(x) <0 на проміжку (а;в), то функція спадає на (а;в). |
|
Питання вчителя |
Очікувана відповідь. |
|
- як знайти точки екстремуму? |
f '(x)=0, якщо f '(x) змінює знак з «+» на «-», то в т. х
якщо f '(x) змінює знак з «-» на «+», то в т. х
|
|
- як знайти точки перетину з осями? |
- з віссю ох: у=0; f (x)=0 - з віссю оу: х=0; у= |
|
- що можна сказати про графік парної функції, непарної функції.
|
|
Учні складають схему дослідження і побудови графіка функції:
- Область визначення функції.
- Точки перетину з осями координат.
- Парність, непарність функції.
- Критичні точки.
- Зростання, спадання функції.
- Точки екстремуму.
- Додаткові точки.
Побудуємо графік функції у=3х![]() -4х
-4х![]() .
.
- Область визначення функції.
х![]()
2. Точки перетину з осями координат. (![]() ; 0); (0;0).
; 0); (0;0).
(ЗРАЗУ ВІДМІЧАЄМО НА КООРДИНАТНІЙ ПЛОЩИНІ !)
3. Парність, непарність функції.
f (-x)= 3х![]() +4х
+4х![]() .
.
Функція ні парна, ні непарна.
- Критичні точки.
f '(x)=0, f '(x)=12 х![]() -12х
-12х![]() ; 12 х
; 12 х![]() -12х
-12х![]() =0;
=0;
х=0; х=1.
5. Зростання, спадання функції.
Функція зростає х![]()
![]() , функція спадає
, функція спадає ![]()
-
Точки екстремуму. х
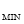 =1: у
=1: у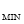 =-1.
=-1.
Відмічаємо на графіку точку (1;-1).
В точці (1;-1) графік має вигляд:

Будуємо графік функції.
Обговорення результату:
|
Питання класу. |
Очікувана відповідь. |
|
При дослідженні функції з’явилася Критична точка х=о. Можливо це точка перегину. Скажіть, як можна з’єднати дві точки, якщо відомо, що функція зростає? Якщо на проміжку (а;в) f ''(x)>0, то f (x) – угнута на проміжку (а;в). Якщо на проміжку (а;в) f ''(x)<0, то f (x) – опукла на проміжку (а;в).
f ''(x |
|
Приклад: Побудувати графік функції у=х![]() .
.
1. Область визначення функції. х![]()
2. Точки перетину з осями координат - (0;0).
3. Парність, непарність функції.
f (-x)= -х![]() . Функція непарна.
. Функція непарна.
4. Критичні точки.
f '(x)=0, f '(x)=3х![]() ; 3х
; 3х![]() =0; х=0;
=0; х=0;
 5. Зростання, спадання функції.
5. Зростання, спадання функції.
Функція зростає х![]()
Можливий графік:

![]()
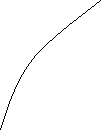
![]()
![]()
![]()
Треба провести дослідження на опуклість, угнутість.
-
 у ''=6х; 6х=0; х=0.
у ''=6х; 6х=0; х=0.
Функція опукла: х![]() , функція угнута х
, функція угнута х![]() .
.
Точка (0;0)- точка перегину.
Отже графік функції у=х![]() має вид:
має вид:
![]()



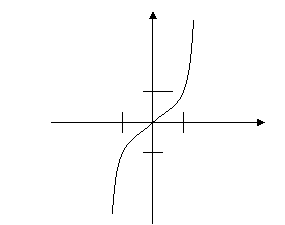
Схему дослідження і побудови графіка функції можна розширити і записати так:
- Область визначення функції.
- Точки перетину з осями координат.
- Парність, непарність функції.
- Дослідження функції за допомогою
Ι похідної. Критичні точки. Зростання, спадання функції. Точки екстремуму.
- Дослідження функції за допомогою ΙΙ похідної. Опуклість, угнутість функції. Точки перегину.
- Додаткові точки.
Давайте повернемося до графіка функції
у=3х![]() -4х
-4х![]()
Проведемо дослідження за допомогою
ΙΙ похідної.
у ''=36 х![]() -24х; 36 х
-24х; 36 х![]() -24х=0; 12х(3х-2)=0; Х=0; х=
-24х=0; 12х(3х-2)=0; Х=0; х=![]() .
.
Функція опукла: х![]() , функція угнута х
, функція угнута х![]() .
.
Точки (0;0), (![]() ) - точки перегину.
) - точки перегину.
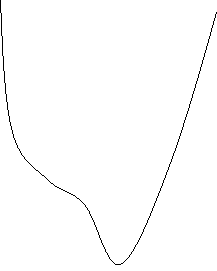

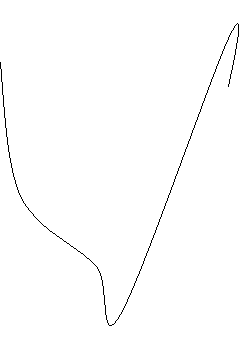
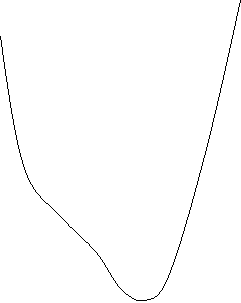 Отже графік функції у=3х
Отже графік функції у=3х![]() -4х
-4х![]() має вид:
має вид:
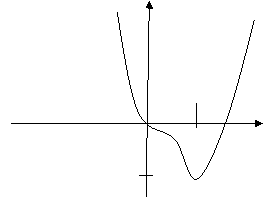

ΙΙΙ-Робота в групах.
Побудувати графіки функцій і перевірити їх побудову за допомогою програми GRAND 2:
Група 1: у=х![]() -3 х
-3 х![]()
Група 2: у=2 х![]() -х
-х![]()
Група 3: у= х![]() -4 х
-4 х![]() .
.
ΙV-Підсумок уроку.
Питання:
- Як побудувати графік функції за допомогою похідної.
- Яку роль грає Ι похідна?
- Яку роль грає Ι Ι похідна?
V- Домашнє завдання.
Дослідити та побудувати графіки функцій:
( N- власний варіант)
-
У=
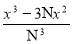 ;
;
-
У=
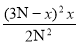 ;
;
-
У=
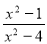 .
.

про публікацію авторської розробки
Додати розробку

