Урок з теми: "Креслення" 11 клас

Урок 9 (1 год)

Тема уроку: Креслення

Мета уроку:навчальна: засвоєння знань про особливості виконання  ортогональних проекцій.

розвиваюча:формування вмінь, технічний світогляд, естетичний смак, пізнавальну та творчу активність.

виховна:виховувати любов до праці, до предмету.

Тип уроку:засвоєння нових знань

Наочність: презентація

Обладнання: Олівці, креслярський інструмент та матеріали: креслярський папір.

Міжпредметні зв'язки: біологія, хімія, образотворче мистецтво, література.

Структура уроку

І. Організаційний момент……………………………………………..	1 хв.
ІІ. Актуалізація опорних знань і вмінь учнів………………………..	6 хв.
ІІІ. Мотивація навчально-пізнавальної діяльності учнів…………... ІV Повідомлення теми та завдань уроку…………………………..	3 хв. 1 хв.
V. Вивчення нового матеріалу………………………………………	10 хв.
VІ. Закріплення нових знань…………………………………………	5 хв.
VІІ. Заключна частина…………………………………………….	5 хв.

 

Хід і зміст уроку

І. Організаційний момент(2 хв.)

1.Введення учнів в майстерню після дзвоника;

2. Привітання;

3 Перевірка присутності учнів за журналом;

4. Перевірка підготовленості учнів до заняття;

5. Ознайомлення учнів з планом заняття.

ІІ. Актуалізація опорних знань і вмінь учнів ( 6 хв)

Під час актуалізації застосовується  прийом «Слухай, розумій, інтерпретуй» Учні працюють зі спеціальними таблицями, у які потрібно записати, як вони розуміють теоретичні поняття, та як саме можуть пояснити їх іншим(Додаток А).

ІІІ. Мотивація навчально-пізнавальної діяльності учнів.

Розповідь вчителя

Наприкінці нашої теми ми з вами будемо створювати лепбуки та кожен буде його захищати. Лепбук або як його ще називають тематична або інтерактивна папка, – це саморобна паперова книжечка з кишеньками, де ви  зможе діставати, складати на свій розсуд різноманітний матеріал. В ній збирається матеріал по якійсь певній темі. При цьому лепбук – це не просто витвір. Це заключний етап самостійної дослідницької роботи, яку ви виконували у ході вивчення даної теми. Щоб заповнити цю папку, вам потрібно буде виконати певні завдання, провести спостереження, вивчити представлений матеріал.

Учитель пропонує учням перелік питань:

1.Яка мені користь від знань про креслення?

2.Чому я сьогодні старанно працюватиму на уроці?

3.Якої мети я хочу досягнути на уроці?

ІV Повідомлення теми та завдань уроку

Тема уроку: Креслення. Завдання уроку:характеризувати особливості виконання  ортогональних проекцій.

V. Вивчення нового матеріалу

Ортогональнапроекція (англ. «orthogonalprojections») — паралельна проекція предмета чи його частини на площині, перпендикулярній до напрямку проекціювальних променів, яка утворює суміщену з креслеником одну з граней порожнистого куба, всередині якого уявно розміщено предмет.

Правила зображення предметів (виробів) на кресленні усіх галузей промисловості та будівництва встановлює міждержавний стандарт ГОСТ 2.305-2008. При побудові ортогональних проекцій за основні площини проекцій беруть шість граней пустотілого куба (паралелепіпеда), всередині якого розміщують предмет, який проекціюється на внутрішні грані куба, утворюючи види, до яких відносяться шість основних видів, що одержують на шести внутрішніх гранях куба:

•     головний вид (вид спереду)— основний вид предмета на фронтальній площині проекцій, який дає найповнішу уяву про його форму і розміри відносно якого розташовують інші основні види;
•     вид зверху;
•     вид зліва;
•     вид справа;
•     вид знизу;
•     вид ззаду.

Види слід виконувати таким чином, щоб головний вигляд давав найповнішу інформацію про предмет. Кількість видів на кресленні залежить від складності предмета. Зображення об'єкта на креслениках повинні давати повне уявлення про його форму, розмірита інші дані, необхідні для його виготовлення та контролю.

Якщо види виконані у проекційному зв'язку та розміщені на своїх традиційних місцях, їх не позначають. Якщо основні види виконані не в проекційному зв'язку та розміщені не на своїх традиційних місцях, то над зображенням ставлять літеру українського алфавіту. Напрямок зору необхідно позначити стрілкою, позначеною такою ж літерою.

Якщо якусь частину предмета (деталі) неможливо показати на основній площині проекцій без спотворення її форм та розмірів, то застосовують допоміжні види:допоміжний вид— вид предмета на площині, непаралельній до жодної з основних площин проекцій, призначений для неспотвореного зображення поверхні, якщо її неможливо 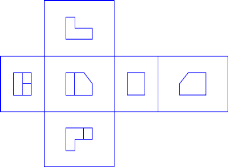отримати на основному виді.

 Зображення окремої, вузько обмеженої частини поверхні деталі називають місцевим видом. Якщо місцевий вид виконується не в проекційному зв'язку, його позначають.

В ортогональних проекціях складається переважна більшість креслеників гірничої та маркшейдерсько-геологічної документації(геологічні карти і розрізи, плани гірничих виробок, профілі рейкових колій, паспорти кріплень тощо).

Ортогональна проекція на вертикальну площину застосовується в маркшейдерській справі для зображення гірничих виробок і документації гірничо-геологічних умов при крутому падінні покладів корисної копалини. Вертикальна площина проекції орієнтується по середньому простяганню покладу.

Ортогональні проекції прямої

1. Завдання прямій на епюрі

Пряма на кресленні може бути задана зображенням прямої, точкою і напрямом, відрізком прямої і двома пересічними площинами.

 

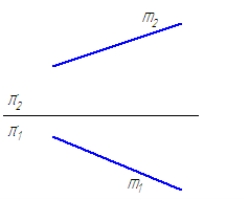
Прямокутної проекцією відрізка в загальному випадку є відрізок (друга властивість центрального і паралельного проектування). На кресленні пряма m (Малюнок.1, а) і відрізок АВ (Малюнок 1, б) довільно нахилені до площин проекцій.

Пряма, що не паралельна жодної з площин проекцій, називається прямою загального положення.

Довжина прямокутної паралельної проекції відрізка загального положення завжди менше довжини самого відрізка.

2. Прямі приватного положення

Пряма, паралельна або перпендикулярна будь-якої площини проекцій, називається пряма приватного положення.

Прямі, паралельні площинам проекцій, називаються прямими рівня.

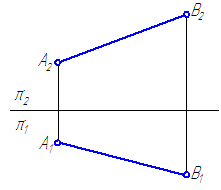
Пряма, паралельна горизонтальній площині проекцій, називається горизонтальною прямою або горизонталлю (Малюнок.2).

Якщо відрізок паралельний площині проекцій π1, то його фронтальна проекція А2В2 паралельна осі проекцій π1 / π2, а горизонтальна проекція відрізка А1В1 визначає справжню величину

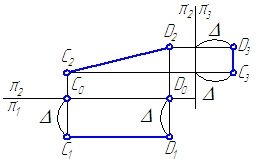АВ:

А2А0 = В2В0

А2В2 || π2 / π1

Пряма, паралельна фронтальній площині проекцій, називається фронтальною прямий або Фронтале (Малюнок 3). Якщо відрізок паралельний площині проекцій π2, то його горизонтальна проекція паралельна осі проекцій π2 / π1, а фронтальна проекція відрізка C2D2 визначає справжню величину CD.

С1А0 = D1D0

C1D1 || π2 / π1 Пряма GH, паралельна профільної площини проекцій, називається профільної прямої (Малюнок 4).

Пряма EF, перпендикулярна горизонтальної площини проекцій, називається горизонтальна (Малюнок 4).

Пряма KL, перпендикулярна фронтальної площини проекцій, називається фронтальна (Малюнок 4).

Пряма MN, перпендикулярна профільної площини проекцій, називається профільна (Малюнок 4).

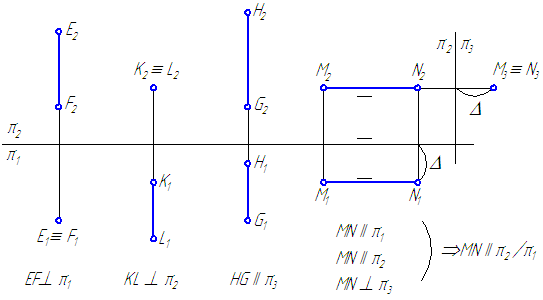
Малюнок 4 - Епюри проекцій прямих (EF, KL, MN) і профільної прямої GH

3. Метод прямокутного трикутника

Метод прямокутного трикутника дозволяє по епюру відрізка прямої загального положення визначити його справжню величину.

Розглянемо положення відрізка АВ відносно горизонтальної площини проекцій π1 (Малюнок 5).

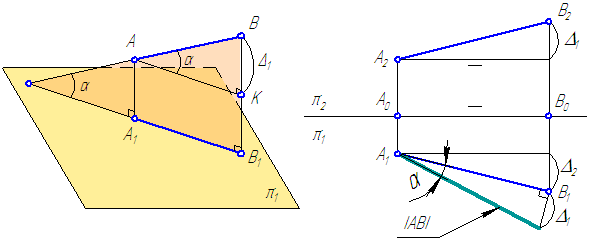
                                     а                                                         б

Малюнок  5 - Визначення дійсної величини відрізка загального положення

На малюнку 5, а:

Аа1 - відстань від точки А до площини проекцій π1;

ВВ1 - відстань від точки В до площини проекцій π1;

А1В1 - проекція відрізка АВ на π1;

∠ (AB; AK) = ∠ (AB; A1B1) = α - кут нахилу прямої АВ до площини проекцій π1.

ΔАКВ - прямокутний трикутник, в якому: АК = А1В1 - катет, що дорівнює горизонтальній проекції відрізка АВ; ВК = ВК = ВВ1 - Аа1 = Δ1 - другий катет, що дорівнює різниці відстаней від кінців відрізка АВ до площини π1 (тобто, різниці координат Z точок А і В); АВ - гіпотенуза ΔАКВ - справжня величина.

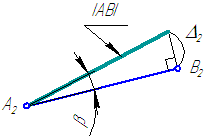При відомих координатах кінців відрізка загального положення можна на епюрі визначити його справжню величину (Малюнок 5, б) на будь-який з площин проекцій.

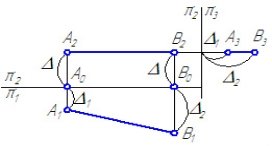
Справжня величина відрізка може бути знайдена як гіпотенуза прямокутного трикутника, одним катетом якого є проекція цього відрізка на площину проекцій (А2В2), а іншим - різниця координат кінців цього відрізка до площини (Δ2), в якій ведеться побудова. Кут між істинною величиною (АВ) і проекцією (А2В2) визначає кут нахилу β прямий до тієї площини проекцій, в якій ведеться побудова (Малюнок 6).

4. Точка і пряма

Якщо точка належить прямій, то її проекції:

-Належать однойменною проекція даної прямої;

-Лежать на одній лінії зв'язку.

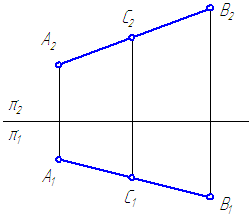
 Точка С належить відрізку АВ (Малюнок 2.7), так як:

С1 ∈ А1В1;

С2 ∈ А2В2;

С1С2 ⊥ π2 / π1;

 

Якщо точка ділить відрізок в будь-якому відношенні, то проекції цієї точки ділять однойменні проекції даного відрізка в тому ж відношенні: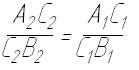

4. Сліди прямої

Слід прямої - точка перетину прямої з площиною проекцій. Пряма загального положення в загальному випадку може бути три сліди:

•                  горизонтальний слід M1- точка перетину прямої з горизонтальною площиною проекцій π1;
•                  фронтальний слід N2- точка перетину прямої з фронтальним площиною проекцій π2;
•                  профільний слід L3 - точка перетину прямої з профільної площиною проекцій π3.

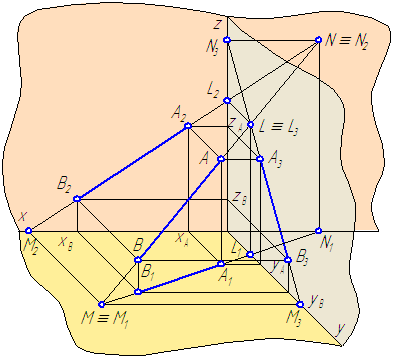Слід прямої є точкою приватного положення, оскільки вона належить площині проекцій, отже, слід прямої завжди збігається з однією зі своїх проекцій: горизонтальний слід збігається зі своєю горизонтальною проекцією M≡M1, фронтальний - з фронтальною проекцією N≡N2, профільний - з профільної проекцією L≡L3 (Малюнок 10).

 

 

 

 

 

 

 

Побудуємо сліди відрізка АВ з площинами проекцій (Малюнки 10, 11). Для побудови горизонтального сліду прямої АВ необхідно:

1.Продовжити фронтальну проекцію прямої АВ до перетину з віссю X, точка перетину М2 є фронтальною проекцією горизонтального сліду;

2.З точки М2 відновити перпендикуляр (лінію проекційної зв'язку) до його перетину з горизонтальною проекцією прямої АВ або її продовженням. Точка перетину М1 і буде горизонтальною проекцією горизонтального сліду, яка збігається з самим слідом М.

Щоб побудувати фронтальний слід відрізка АВ прямої, необхідно:

1.Продовжити горизонтальну проекцію прямої АВ до перетину з віссю X, точка перетину N1 є горизонтальною проекцією фронтального сліду;

2. З точки N1 відновити перпендикуляр (лінію проекційної зв'язку) до його перетину з фронтальною проекцією прямої АВ або її продовженням. Точка перетину N2 і буде фронтальною проекцією фронтального сліду, яка збігається з самим слідом N.

Алгоритм побудови слідів відрізка прямої АВ:

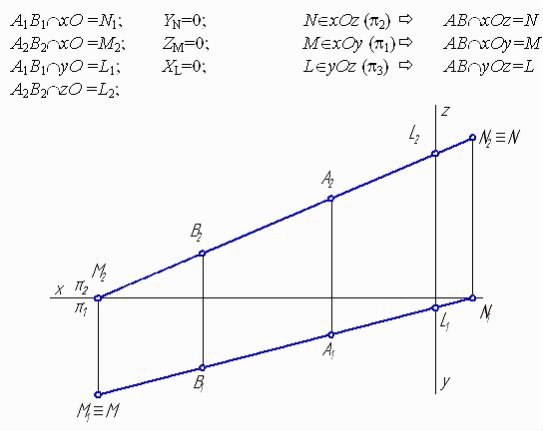
Малюнок 11 - Епюр побудови слідів відрізка прямої АВ

Пряма, паралельна одній з площин проекцій, не має сліду на площині, якій вона паралельна, і перетинає тільки дві площини. Пряма, паралельна двох площинах проекцій (проектує пряма), має тільки один слід, що співпадає з проекцією прямої на площину, до якої вона перпендикулярна.

5. Взаємне розміщення прямих

Дві прямі в просторі можуть бути: паралельними; пересічними; перехресними.

Паралельні прямі - прямі, що перетинаються в невласне точці. Якщо прямі в просторі паралельні, то їх ортогональні проекції взаємно паралельні, або зливаються, або представляють собою точки, на одній з площин проекцій (Малюнок 12).

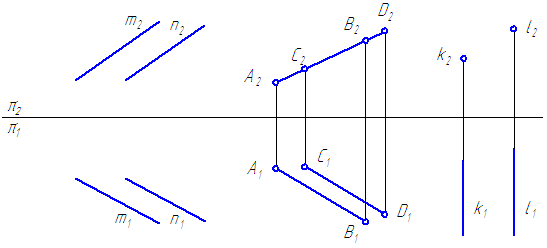
Малюнок 12 - Паралельні прямі

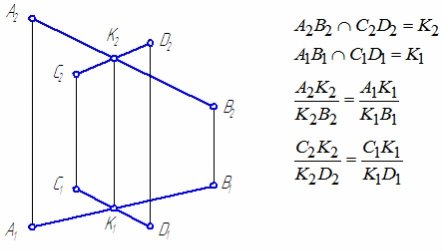Пересічні прямі - прямі, що мають одну спільну точку. Якщо прямі в просторі перетинаються, то на кресленні однойменні проекції прямих перетинаються, при цьому проекції точки перетину прямих лежать на одній лінії проекційної зв'язку і ділять відповідні проекції відрізків прямих в рівних відносинах (Малюнок 13).

 

 

 

 

 

 

Малюнок 13 - Пересічні прямі

 

Перехресні прямі - прямі, що не мають спільних точок (Малюнок 14). Ознака перехресних прямих: однойменні проекції перетинаються, точки перетину проекцій чи не лежать на одній лінії зв'язку.

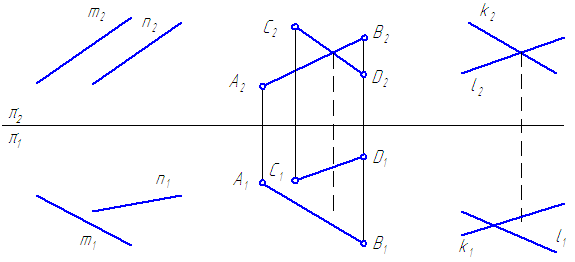
Малюнок 14 - Перехресні прямі

VІ. Закріплення нових знань

Вправа 1. Розділити точкою До відрізок EF в співвідношенні EK: KF = 1: 3 (Малюнок 15)

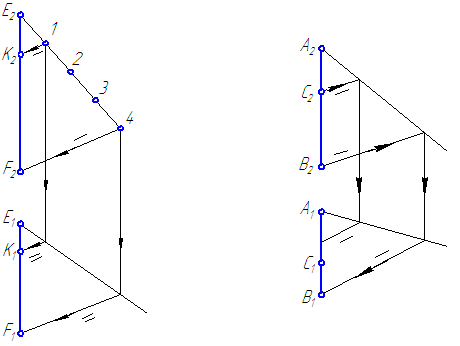
Малюнок 15                                                             Малюнок 16

Рішення:

Проведемо довільну пряму з будь-якого кінця будь-якій проекції відрізка, наприклад, Е2.

Відкладемо на цій прямій від точки Е2 рівні відрізки, кількість яких дорівнює сумі чисел, що становлять дріб (в нашому прикладі 1 + 3 = 4).

З'єднаємо останню крапку 4 з іншим кінцем фронтальної проекції відрізка - точкою F2.

З точки 1 проведемо пряму, паралельну прямій (4-F2) до перетину з проекцією E2F2, таким чином буде знайдено фронтальна проекція шуканої точки К2.

Горизонтальну проекцію точки К1 отримаємо шляхом побудови лінії проекційної зв'язку до перетину її з горизонтальною проекцією відрізка.

Вправа 2. Визначити приналежність точки С відрізку прямої АВ (Малюнок 16).

Відповідь: точка С не належить відрізку АВ, так як не виконується умова приналежності точки прямої.

Завдання 1. Визначте взаємне положення прямих і побудуйте перетин прямих АВ і CD прямий EF // π2 / π1 (Малюнок 17).

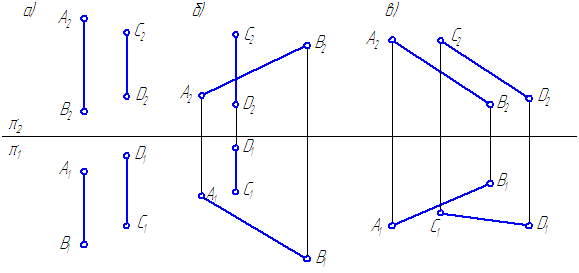
Малюнок 17

Завдання 2. Побудувати відрізок прямої АВ // π1, рівний 35 мм і нахилений до π2 під кутом 25 ° (Малюнок 16).

Завдання 3. Побудувати відрізок прямої CD за координатами його кінців С (20; 15; 30), D (70; 40; 15) і визначити справжню величину відрізка і кути нахилу його до площин проекцій π2 і π1.

Завдання 4. Побудуйте проекції відрізків приватного положення, розташованих під кутом 30 ° до площини проекцій π1 і 45 ° - до площини проекцій π2.

VІІ. Заключна частина

ПІДВЕДЕННЯ ВЧИТЕЛЕМ ПІДСУМКІВ ЗАНЯТТЯ

1.Вчитель повідомляє про досягнення цілей заняття;

2. Проведення об’єктивної оцінки результатів роботи; виставлення оцінок у класний журнал та щоденники учнів;

Домашнє завдання: Повторити матеріал, який вивчили на уроці.