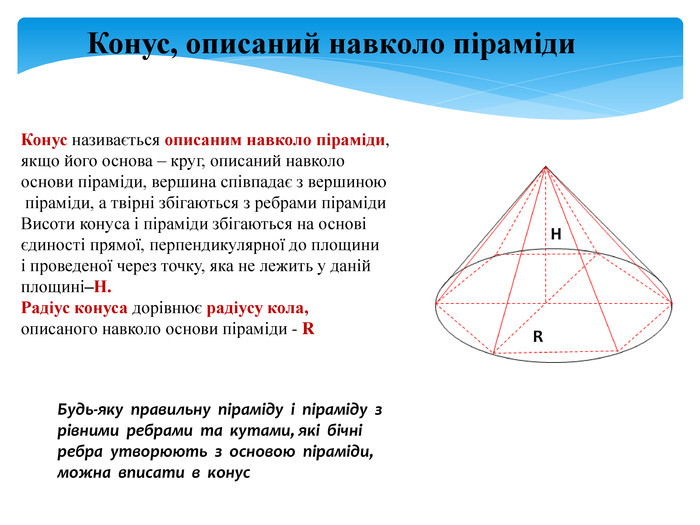
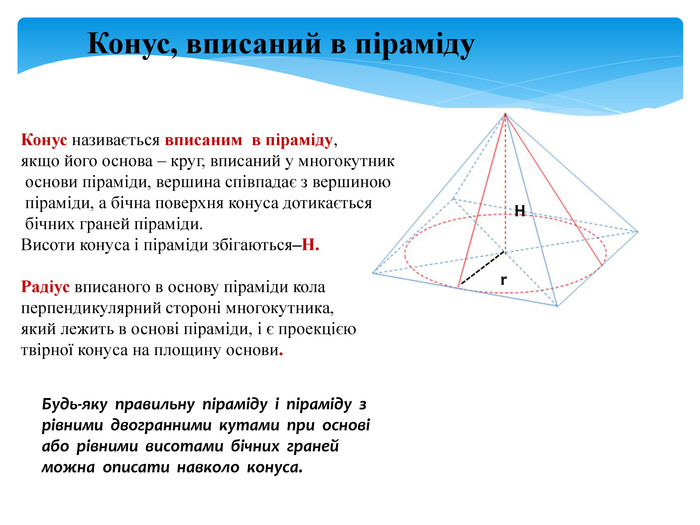
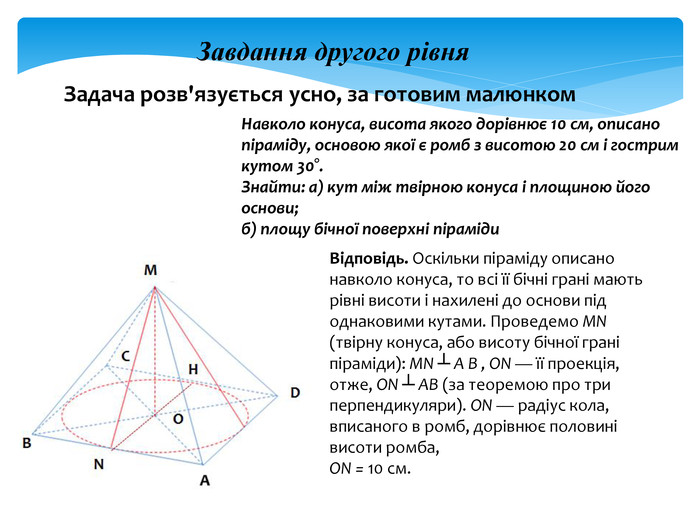
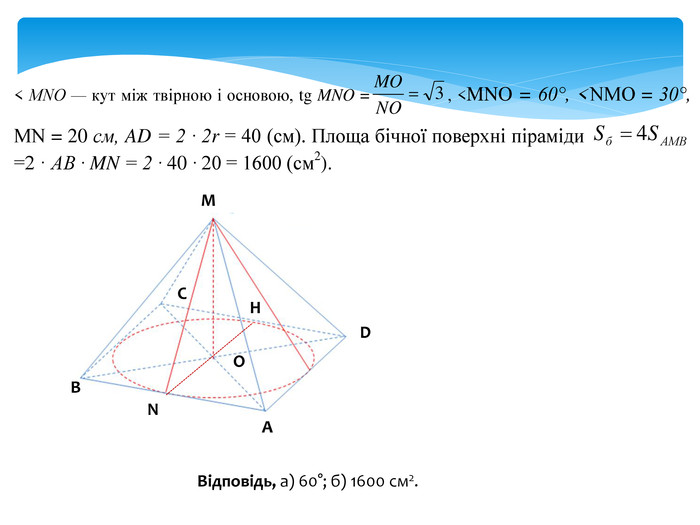
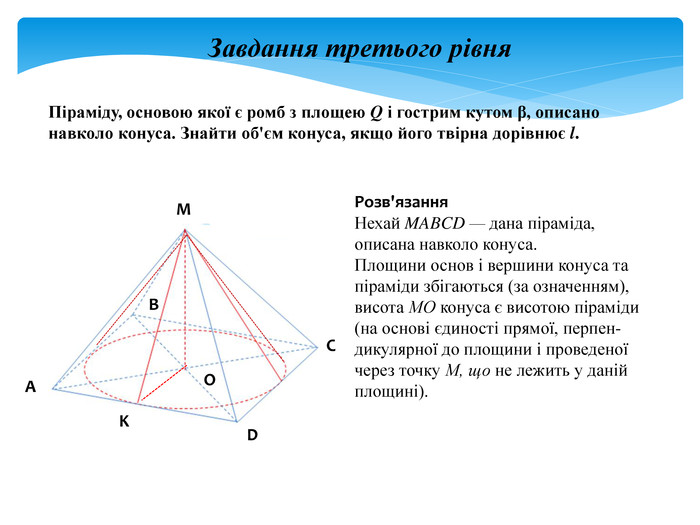
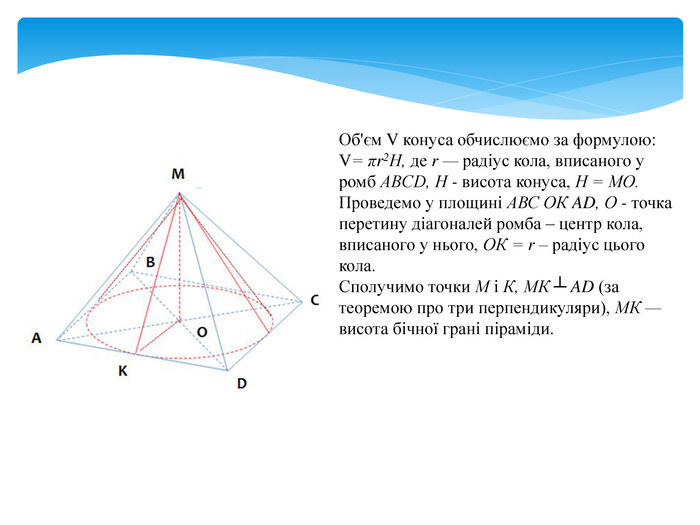
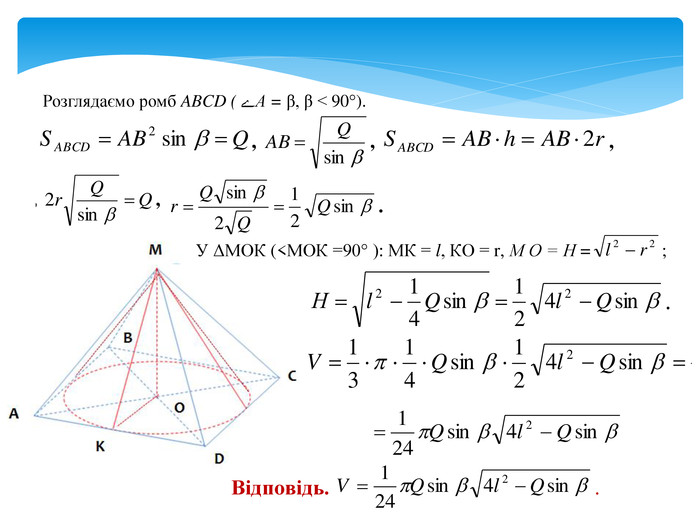
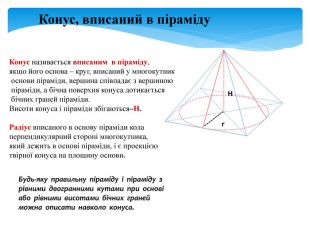
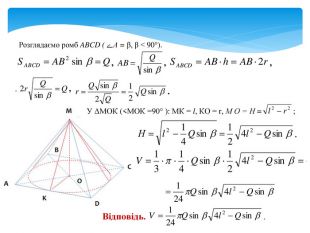
задачі на комбінацію конуса і піраміди
Про матеріал
Дана презентація допоможе учням закріпити знання з теми "комбінації тіл у просторі"
Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку