Заняття №13-14 на тему «Цілі вирази, їх види. Многочлени, ділення многочленів»

Заняття №13-14 на тему «Цілі вирази, їх види. Многочлени, ділення многочленів»

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв'язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

 

Тема 2. Цілі вирази та їх перетворення

Заняття 13-14

Цілі вирази, їх види. Многочлени, ділення многочленів

Використовуючи знаки дій і дужки, можна з чисел і букв складати математичні вирази. Наприклад:

3а²в; . Математичні вирази класифікуються за характером математичних операцій.

Математичні вирази, які містять дії додавання, віднімання, множення, ділення і піднесення до степеня з цілим показником, називаються раціональними виразами.

Раціональні вирази
Цілі вирази – вирази, які не містять букв у знаменнику. Наприклад, 2т;	Дробові вирази – вирази, які містять букви в знаменнику. Наприклад, .

Цілий вираз має зміст при будь-яких значеннях змінних, що входять до нього. Дробовий вираз при деяких значеннях змінної може не мати змісту. Наприклад, вираз втрачає зміст, коли а=2. Ділити на нуль не можна.

Значення змінних, при яких можливі всі математичні дії, що містяться у виразі, називаються допустимими значеннями змінних. Вони утворюють область визначення або область допустимих значень змінних (скорочено ОДЗ).

Наприклад, ОДЗ виразу є значення змінних, коли

Многочлен Р(х)  відносно змінної х виду

, де а₀,  а₁, а₂,… а_п – деякі числа  і , називають многочленом степеня п, розміщеним за спаданням степенів х, або многочленом , записаним в канонічному стандартному вигляді. Числа а₀, а₁, а₂,…, а_п називають коефіцієнтами многочлена.

Якщо многочлени , , такі, що справедлива рівність =·, то говорять, що кожний із многочленів і є дільником многочлена . При цьому вважають, що многочлен ділиться (націло) на многочлен (або).

Нижні коефіцієнти біля букв, що позначають  многочлени, вказують на степінь многочлена.

Способи ділення многочленів:

1.   Метод невизначених коефіцієнтів;
2.   Ділення в «стовпчик» («кутом»);
3.   Схема Горнера

Розглянемо один із способів ділення многочленів.

Ділення многочленів виконується аналогічно до ділення багатоцифрових чисел. Розглянемо спочатку ділення многочленів з однією змінною. Ділення можливе у тому випадку, коли степінь многочлена - діленого вищий або дорівнює степеню многочлена - дільника. Перед діленням многочлена на многочлен кожний з них записують у стандартному вигляді, потім ділять старший член діленого на старший член дільника, частку від ділення старших членів множать на дільник і цей добуток віднімають від діленого; різницю, що дістали (першу остачу), знову аналогічно ділять на дільник і знаходять другий член частки. Цей процес продовжують доти, поки ділення не закінчиться (в остачі буде 0) або степінь остачі буде нижчим від степеня дільника.

Розв'язування задач і вправ.

•             Поділити х⁴ + 2х³ – 3х² + 5х – 1 на х² – 2х + 2.

Розв’язання:

 х⁴ + 2х³ – 3х² + 5х – 1   х² – 2х + 2

 х⁴ – 2х³ + 2х²                  х² + 4х + 3

        4х³ – 5х² + 5х

        4х³ – 8х² + 8х 

                 3х² – 3х – 1

                 3х² – 6х + 6  

                           3х – 7

За аналогією з діленням чисел ми можемо записати:

х⁴ + 2х³ – 3х² + 5х – 1 = (х² – 2х + 2) (х² + 4х +3) + (3х – 7)

або =

•             Поділити 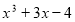на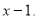 

Розв’язання:

             

        

                 

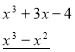
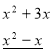
                                       0 

Можемо записати:

•        Поділити 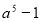на а – 1.

Розв’язання:

-                  

       -

                -

                         -

                                 -

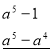
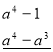
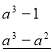
                                         0

Звідси дістанемо: 

Коли ділимо многочлен з кількома змінними, одну з них приймаємо за змінну, а всі інші – за сталі.

•        Поділити 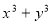на   .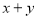

Розв’язання:

-                        

         -

                       - 

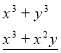
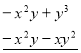
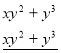
                                     0

Дістанемо:  - формула суми кубів двох чисел.

Завдання для самостійного розв’язування.

1. Виконати ділення:

a) х⁵+ у⁵ на х+ у;

b) х⁵- у⁵ на х- у;

c) а³+в³+с³ -3авс на а+в+с;

2. Спростити вираз:

a)

b)

3. Розкласти многочлен х³+х-2 на множники, якщо відомо, що він ділиться на х-1.

 

 

 Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.